Прямая линия и точка в плоскости общего положения
Из аксиомы принадлежности известно, что прямая принадлежит плоскости, если две точки этой прямой принадлежат той же плоскости.
На рис. 4.5а плоскость задана двумя пересекающимися прямыми (m Ç n).
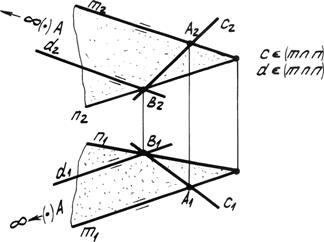
Рис. 4.5а.
На заданных прямых отметим две произвольные точки А и В, которые определят прямую с, принадлежащую плоскости (m Ç n). Если одна из точек, например А, удалена в бесконечность, т.е. является несобственной, то аксиома принадлежности формулируется так:
Прямая линия принадлежит плоскости, если имеет с ней общую точку и параллельна какой-либо прямой, лежащей в плоскости. В данной плоскости (m Ç n) прямая d параллельна прямой m и проходит через точку В.
При задании плоскости следами (рис. 4.5б, в) две точки, определяющие принадлежность прямой линии плоскости, будут следами этой прямой линии. На рис. 4.5б фронтальный след N прямой l расположен на фронтальном следе плоскости l2, а горизонтальный след М – на горизонтальном следе плоскости l1.

Рис. 4.5б.
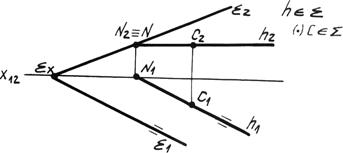
Рис. 4.5в.
На тех же примерах рассмотрим точку в плоскости.
Точка принадлежит плоскости если она расположена на прямой, принадлежащей плоскости. Отметим на прямой l (рис. 4.5б) точку 1, а на прямой h (рис. 4.5в) точку С. Точка 1 будет принадлежать плоскости l, а точка С – плоскости S, т.к. расположены на прямых, принадлежащим соответствующим плоскостям.
Дата добавления: 2015-09-11; просмотров: 709;
