ГЛАВА 2. ТОЧКА

2.1. Ортогональная система двух плоскостей проекций.
Эпюр Монжа

Ортогональное или прямоугольное проецирование является частным случаем параллельного (косоугольного) проецирования. Направление проецирующих лучей в ортогональном проецировании перпендикулярно плоскости проекций.

Метод ортогонального проецирования на две взаимно перпендикулярные плоскости носит название метода Монжа. Гаспар Монж (1746 - 1818 г.) – француз, основоположник начертательной геометрии.

Зададим две взаимно перпендикулярные плоскости проекций p₁ ^ p₂ (рис. 2.1) p₁ – горизонтальная плоскость проекций, p₂ – фронтальная плоскость проекций. Линия пересечения плоскостей называется осью проекций и обозначается х₁₂.

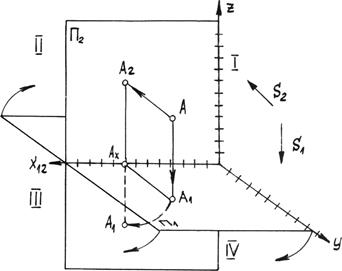
Рис. 2.1. Система 2^х плоскостей проекций.

Четыре двухгранных угла, на которые плоскости делят пространство, называются четвертями.

Спроецируем точку А, произвольно выбранную в первой четверти, в данной системе плоскостей проекций. Направление лучей проецирования s₁ перпендикулярно p₁ и s₂ перпендикулярно p₂. А₁ – горизонтальная проекция точки А, А₂ – фронтальная проекция точки А. Проецирующие лучи АА₁ и АА₂ образуют плоскость, которая пересекает плоскость проекций по прямым А_хА₁ и А_хА₂. Эти прямые перпендикулярны оси x₁₂ и называются линиями проекционной связи.

Повернем плоскость p₁ вокруг оси x₁₂ до совмещения с p₂ на 90° в направлении, указанном на чертеже (рис. 2.1). Получим одну плоскость – плоскость чертежа или эпюр (фр. - чертеж) (рис. 2.2).

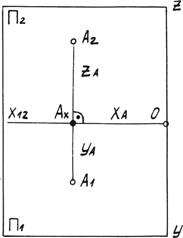
Рис. 2.2. Эпюр точки.

Эпюром точки называется чертеж, на котором изображены две проекции точки, расположенные в проекционной связи.

Две проекции точки вполне определяют ее положение в пространстве. Если из проекции А₁ и А₂ восстановить перпендикуляры к плоскостям проекций, то точка А определится однозначно. Точка А в пространстве определена тремя координатами x, y, z, которые можно измерять на эпюре.