Активная точка зрения.

Обозначим (рис. 3.1), 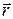‑ некоторый вектор, 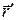‑ этот же вектор повернутый вокруг оси Oz на угол ψ, 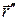‑ это вектор 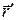, повернутый вторым поворотом (на рис 3.1 не показан).

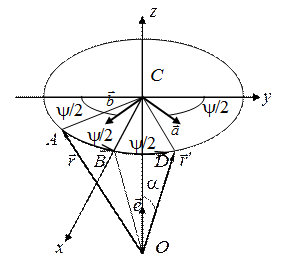
Рис. 3.1

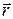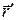При этом угол с осью Oz у векторов и один и тот же, т.е. a, так как при повороте вектор 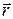описывает круговую коническую поверхность. В этом случае кватернион, соответствующий такому повороту, примет вид

.

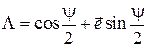Найдем кватернионные произведения 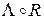и 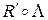, считая R и R’ ква-тернионами, получаемыми из 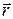и 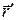добавлением нулевой скалярной части, т.е. представляя их в виде 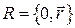, 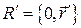. Получим

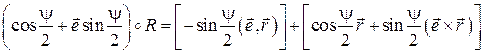
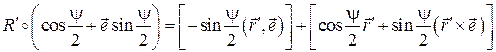
Легко видеть, что скалярные части полученных кватернионов одинаковы, т.к. 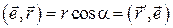. Но одинаковы и векторные части. Для доказательства этого запишем проекции этих частей на оси системы координат, изображенной на рис. 4.1 (ось Cz есть ось конечного поворота тела на угол ψ, а ось Cx является биссектрисой угла ψ). Имеем

, ,

, ,

,

.

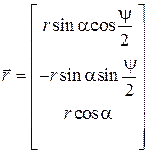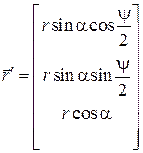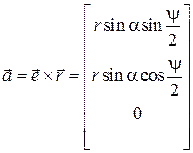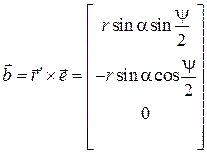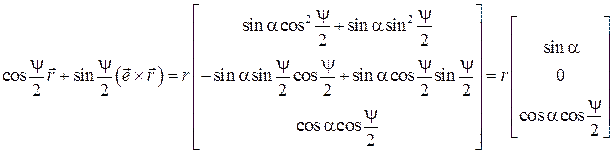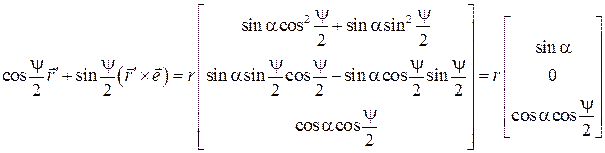Таким образом, мы получили, что 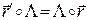. Откуда следует

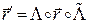. (3.1)

Это выражение можно сравнить с формулой преобразования координат вектора с помощью матрицы поворота L при его повороте

.

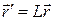При этом элементы такой матрицы выразятся через компоненты кватерниона Λ следующим образом

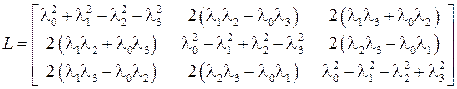(3.2)

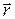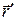Тогда, если ввести кватернион второго поворота вектора (от к )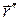

,

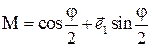то, аналогично, получим .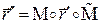

Поэтому

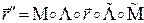
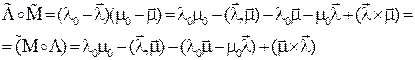
То есть,

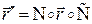
Значит, 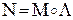‑ результирующий кватернион, описывающий два поворота вектора 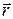, равен произведению кватернионов слагаемых поворотов в обратном порядке относительно последовательности поворотов.