Критериальные уравнения
Применяя общие законы физики, можно составить дифференциальные уравнения для конвективного теплообмена, учитывающие как тепловые, так и гидродинамические явления в любом процессе.
Система дифференциальных уравнений состоит из 6 уравнений: энергии (или теплопроводности), теплообмена, движения (3 уравнения) и уравнение сплошности.
В результате анализа этих уравнений получены критерии подобия и критериальные уравнения, которые используются при исследовании конвективного теплообмена.
Критериальным уравнением называют зависимость между каким-либо определяемым критерием подобия и другими определяющими критериями подобия.
При расчете тепловых аппаратов искомыми величинами являются коэффициент теплоотдачи 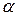 и гидравлическое сопротивление
и гидравлическое сопротивление 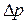 . Конвективный теплообмен характеризуется пятью критериями подобия – Nu, Eu, Pr, Gr и Re.
. Конвективный теплообмен характеризуется пятью критериями подобия – Nu, Eu, Pr, Gr и Re.
Критерий Нуссельта (Nu) содержит искомый коэффициент теплоотдачи 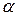 , а критерий Эйлера (Eu) – искомую величину
, а критерий Эйлера (Eu) – искомую величину 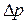 , характеризующую гидравлическое сопротивление при движении жидкости. Поэтому критерии Nu и Eu являются определяемыми критериями подобия, а критерии Прандтля (Pr), Грасгофа (Gr) и Рейнольдса (Re) – определяющими.
, характеризующую гидравлическое сопротивление при движении жидкости. Поэтому критерии Nu и Eu являются определяемыми критериями подобия, а критерии Прандтля (Pr), Грасгофа (Gr) и Рейнольдса (Re) – определяющими.
При конвективном теплообмене критериальные уравнения могут быть представлены в следующем виде:
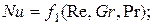 (4.6)
(4.6)
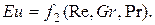 (4.7)
(4.7)
Зависимость между критериями в основном определяется опытным путем.
В случае вынужденного движения жидкости и при развитом турбулентном режиме свободная конвекция в сравнении с вынужденной очень мала, поэтому критериальное уравнение теплоотдачи упрощается:
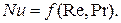 (4.8)
(4.8)
Для некоторых газов величина критерия Прандтля в процессе конвективного теплообмена почти не изменяется с температурой, поэтому критериальное уравнение принимает более простой вид:
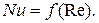 (4.9)
(4.9)
При свободном движении жидкости, когда вынужденная конвекция отсутствует, вместо критерия Рейнольдса в критериальное уравнение теплоотдачи необходимо ввести критерий Грасгофа. При этом получается зависимость:
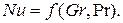 (4.10)
(4.10)
При исследовании теплообмена капельных жидкостей и газов со стенкой оказывается, что теплоотдача будет различной в условиях нагревания и охлаждения. Это явление связано с изменением физических параметров жидкости в пограничном слое. Для получения критериальных уравнений, одинаково справедливых как для нагревания, так и для охлаждения, вводят дополнительно отношения:
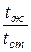 ,
, 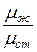 ,
, 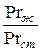 . (4.11)
. (4.11)
Первое соотношение обычно применяют при расчете теплоотдачи газов, остальные два – при расчете теплоотдачи капельных жидкостей.
Академик М.А. Михеев рекомендует учитывать направление теплового потока отношением 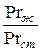 . Тогда общее критериальное уравнение для конвективного теплообмена принимает следующий вид:
. Тогда общее критериальное уравнение для конвективного теплообмена принимает следующий вид:
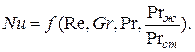 (4.12)
(4.12)
В такой же форме можно представить все уравнения для частных случаев. Количественная связь между критериями подобия и является предметом экспериментальных исследований.
Вопросы для самоконтроля к разделу 4
1. Что называется конвективным теплообменом?
2. Какие различают виды конвекции?
3. Гидродинамический и тепловой пограничные слои и их физический смысл.
4. Какие встречаются виды движения жидкости и их различие?
5. Критерий Рейнольдса и его обозначение.
6. Какова размерность критерия Рейнольдса?
7. Критическое значение критерия Рейнольдса.
8. Каков механизм передачи теплоты при ламинарном и турбулентном движении
жидкости?
9. Дать определение динамической и кинематической вязкости.
10. Какие факторы влияют на конвективный теплообмен?
11. Определение коэффициента теплоотдачи.
12. Функцией каких величин является коэффициент теплоотдачи?
13. Что называется условиями однозначности?
14. Почему для определения коэффициента теплоотдачи применяют теорию
подобия?
15. Какие условия лежат в основе теории подобия?
16. От каких величин зависит коэффициент теплоотдачи?
17. Какие критерии подобия получают из дифференциальных уравнений
конвективного теплообмена?
18. Какое уравнение называется критериальным?
19. Какими критериями подобия характеризуется конвективный теплообмен
для газов и капельных жидкостей?
Дата добавления: 2015-09-02; просмотров: 7390;
