Краевые условия

Полученное дифференциальное уравнение Фурье описывает яв­ления передачи, теплоты теплопроводностью в самом общем виде. Для того чтобы применить его к конкретному случаю, необходимо знать распределение температур в теле в начальный момент времени или начальные условия. Кроме того, должны быть известны: гео­метрическая форма и размеры тела, физические параметры среды и тела и граничные условия, характеризующие распределение тем­ператур на поверхности тела, или взаимодействие изучаемого тела с окружающей средой. Все эти частные особенности совместно с дифференциальным уравнением дают полное описание конкретного про­цесса теплопроводности и называются условиями однозначности, или краевыми условиями.

Обычно начальные условия распределения температуры задаются для момента времени 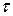= 0.

Граничные условия могут быть заданы тремя способами.

Граничное условие первого рода задается распределением темпе­ратуры на поверхности тела для любого момента времени.

Граничное условие второго рода задается плотностью теплового потока в каждой точке поверхности тела для любого момента времени.

Граничное условие третьего рода задается температурой среды, окружающей тело, и законом теплоотдачи между поверхностью тела и окружающей средой.

Законы конвективного теплообмена между поверхностью тела и окружающей средой отличаются большой сложностью. В основу изучения конвективного теплообмена положен закон Ньютона – Рихмана:

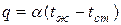, (1.11)

где q – плотность теплового потока, Вт/м ;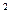

t 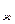– температура окружающей среды (жидкости), °С;

t 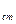– температура поверхности тела (стенки), °С;

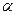– коэффициент пропорциональности, называемый коэф­фициентом

теплоотдачи, Вт/ м 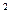град.

Коэффициент теплоотдачи характеризует интенсивность тепло­обмена между поверхностью тела и окружающей средой. Он чис­ленно равен количеству теплоты, отдаваемой (или воспринимаемой) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в 1°. Коэффициент теплоотдачи зависит от многих факторов, но при решении задач теплопроводности твердого тела его принимают в большинстве слу­чаев величиной постоянной.

Согласно закону сохранения энергии, количество теплоты, от­даваемое единицей поверхности тела окружающей среде в единицу времени вследствие теплоотдачи, должно быть равно теплоте, кото­рая путем теплопроводности подводится к единице поверхности в единицу времени со стороны внутренних частей тела, т. е.

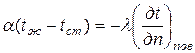(1.12)

где 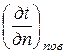– проекция температурного градиента на направление нормали к

площадке dF; индекс «пов» пока­зывает, что температурный

градиент относится к поверхности тела.

Равенство (1.12) является математической формулировкой гра­ничного условия третьего рода; оно является действительным для каждого момента времени.

Решение дифференциального уравнения теплопроводности при заданных условиях однозначности позволяет определить темпера­турное поле во всем объеме тела для любого момента времени или найти функцию:

t = f (х, у, z, ).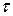

Вопросы для самоконтроля к разделу 1

1. Назовите основные случаи теплообмена.

2. Опишите подробно все виды теплообмена.

3. Что называется конвективным теплообменом?

4. Какова природа лучистой энергии и передача теплоты излу­чением?

5. Что называется сложным теплообменом?

6. Что называется температурным полем? Написать его урав­нение.

7. Уравнение температурного поля при стационарном режиме.

8. Уравнение одномерного температурного поля.

9. Что называется температурным градиентом?

10. Закон Фурье.

11. Что называется коэффициентом теплопроводности?

12. Описать особенности теплопроводности различных веществ.

13. Уравнение Фурье для трехмерного температурного поля.

14. Что называется коэффициентом температуропроводности?

15. Какими величинами задаются граничные условия первого, второго и третьего

рода?

16. Закон Ньютона – Рихмана.

17. Что называется коэффициентом теплоотдачи?