Введение. Дифракция в первоначальном узком смысле – огибание волнами препятствий; в современном более широком–любое отклонение при распространении волн в неоднородных

Дифракция в первоначальном узком смысле – огибание волнами препятствий; в современном более широком–любое отклонение при распространении волн в неоднородных средах от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени. Дифракционные явления не зависят от природы дифрагирующих полей и доказывают, что материя, в частности свет, обладает волновыми свойствами.

В настоящей работе дифракция света происходит на дифракционной решетке. Под дифракционной решеткой подразумевается любая конечная совокупность неоднородностей среды, создающая периодическое изменение амплитуды и фазы проходящей сквозь нее волны. Амплитудные решетки периодически изменяют амплитуды дифрагирующих волн за счет периодически изменяющихся пропускающих свойств решетки (чередования прозрачных и непрозрачных полос). Фазовые – периодически изменяют фазы дифрагирующих волн за счет периодически изменяющихся геометрических размеров либо преломляющих свойств решетки (чередования однородных областей разной толщины, или областей с разными показателями преломления).

Наиболее отчетливо дифракция проявляется, когда размеры неоднородностей сравнимы с длиной волны. Структура дифракционного поля зависит от расстояния L между решеткой и точкой наблюдения.

В работе изучается дифракция Фраунгофера, то есть дифракция плоскопараллельных волн на неоднородностях среды при условии

lL >> D²,

где D– характерный размер неоднородности;

l – длинаволны, L – расстояние между решеткой и точкой наблюдения.

Рассмотрим дифракцию Фраунгофера на одной щели бесконечной длины. Предположим, что на щель падает плоскопараллельная монохроматическая световая волна (рис. 1), распространяющаяся в направлении X со скоростью u перпендикулярно плоскости щели (нормальное падение). Ширина щели a сравнима с длиной волны l.

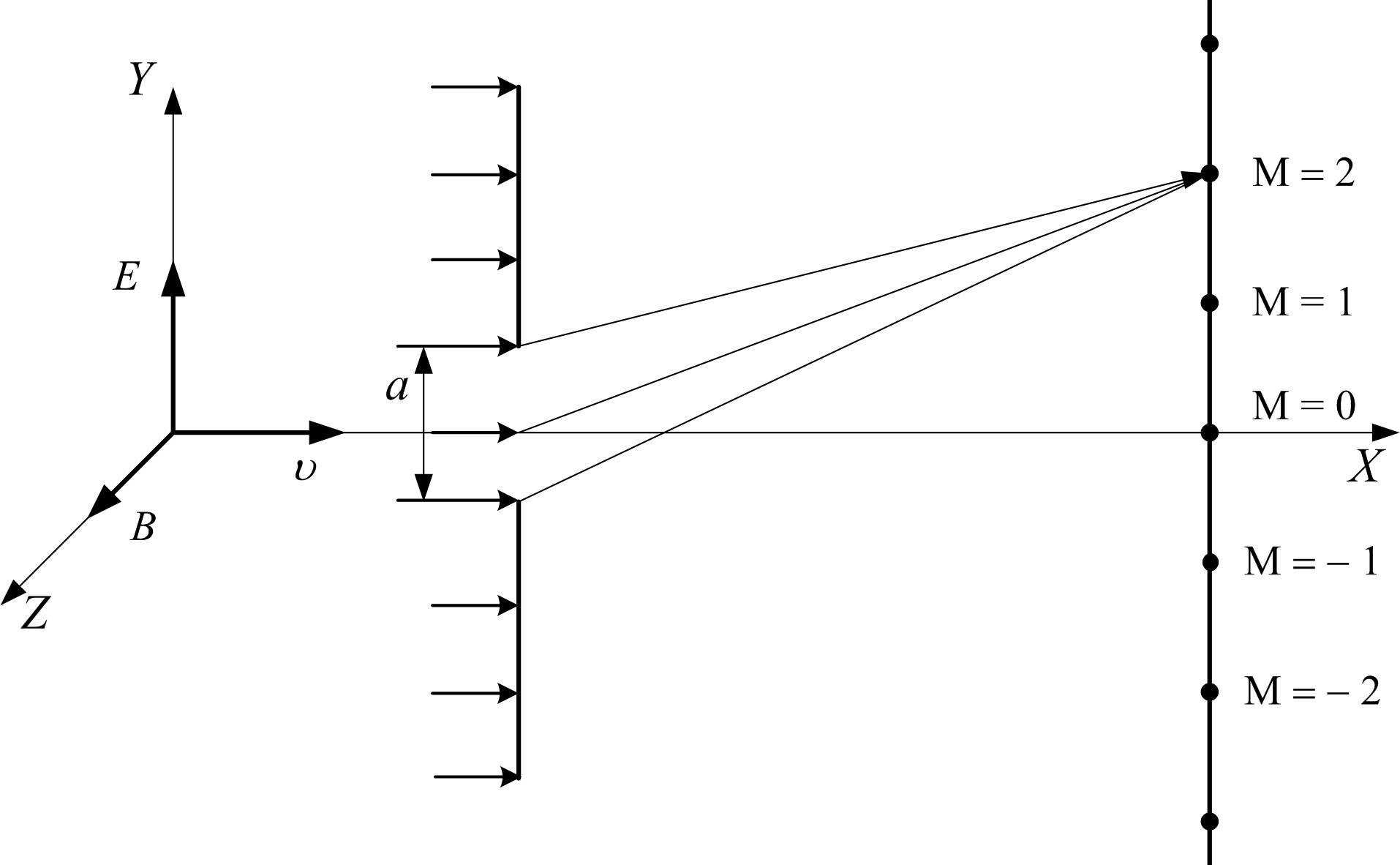
Рис. 1.

В соответствии с принципом Гюйгенса каждая точка волновой поверхности (поверхности одинаковой фазы колебаний) является точечным источником вторичных полусферических волн. В случае нормального падения на щель когерентных плоскопараллельных волн плоскость щели совпадает с волновой поверхностью и испускает во всех направлениях бесконечное число вторичных полусферических волн одинаковой фазы, так называемые дифрагированные волны, распространяющиеся в область геометрической тени. Таким образом, в области за щелью возникает волновое электромагнитное (дифракционное) поле, которое можно рассматривать как результат суперпозиции бесконечного числа дифрагированных на щели полусферических электромагнитных, в нашем случае когерентных волн вида

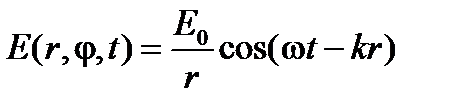, (1)

где E₀ – амплитуда электрических световых волн в плоскости щели;

r – радиус-вектор, проведённый от точечного источника вторичной волны к данной точке поля;

w – круговая частота колебаний источника света;

k – волновой вектор.

При сложении этих волн в достаточно удаленной точке поля на какой-либо произвольной поверхности, например на оптическом экране, мы сможем наблюдать их устойчивую интерференцию в виде так называемой дифракционной картины или дифракционного спектра с чередующимися максимумами и минимумами излучения, убывающими по интенсивности. Интенсивность освещенности любой точки дифракционной картины определится квадратом амплитуды результирующего колебания в данной точке.

Распределение интенсивности в дифракционной картине с достаточной степенью точности может быть получено приближенным методом Гюйгенса-Френеля, в соответствии с которым поверхность щели разбивается на так называемые зоны Френеля, в нашем случае — на бесконечно длинные полосы, так что оптическая разность хода лучей, идущих от краев одной зоны Френеля к рассматриваемой точке поля, равна l/2.

Если считать, что зоны Френеля излучают энергию во всех направлениях одинаково, то при сложении в любой точке экрана колебаний от четного числа зон Френеля, равных по амплитуде и противоположных по фазе, получим дифракционный минимум, т. е. освещенность, равную нулю. При сложении в любой точке экрана колебаний от нечетного числа зон Френеля получим дифракционный максимум, интенсивность освещенности которого определится результирующим колебанием от одной, не скомпенсированной зоны Френеля.

Условия минимума и максимума освещенности различных точек экрана при интерференции волн, дифрагированных одной щелью шириной a, в соответствии с принципом Гюйгенса-Френеля записываются в виде:

условие минимума

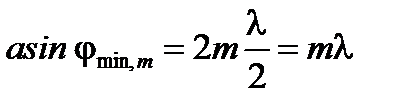; (2)

условие максимума

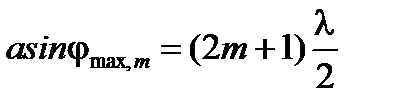, (2¢)

где m = 0; ±1; ±2; ± 3... – любое целое число, определяющее порядок минимумов и максимумов;

j_m – угол наблюдения максимума или минимума m-го порядка по отношению к нормали (угол дифракции).

Распределение интенсивности в дифракционной картине от одной щели в направлении y может быть выражено функцией вида

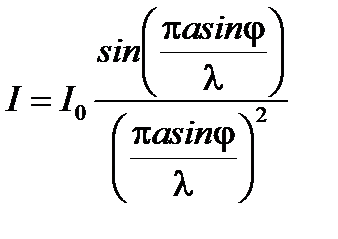, (3)

I₀ – интенсивность освещенности в центральной точке дифракционной картины, т. е. под углом дифракции j₀ = 0 для m = 0. Из выражений (2') и (3) следует, что в центре дифракционной картины от одной щели всегда наблюдается максимум интенсивности, а с ростом m, то есть с ростом углов дифракции, интенсивность максимумов уменьшается.

Рассмотрим дифракцию Фраунгофера при нормальном падении монохроматической световой волны на решетку, состоящую из N одинаковых бесконечно длинных параллельных щелей шириной a, расположенных на расстоянии b друг от друга. Величина d = a + b называется постоянной или периодом дифракционной решетки вдоль направления y (рис. 2).

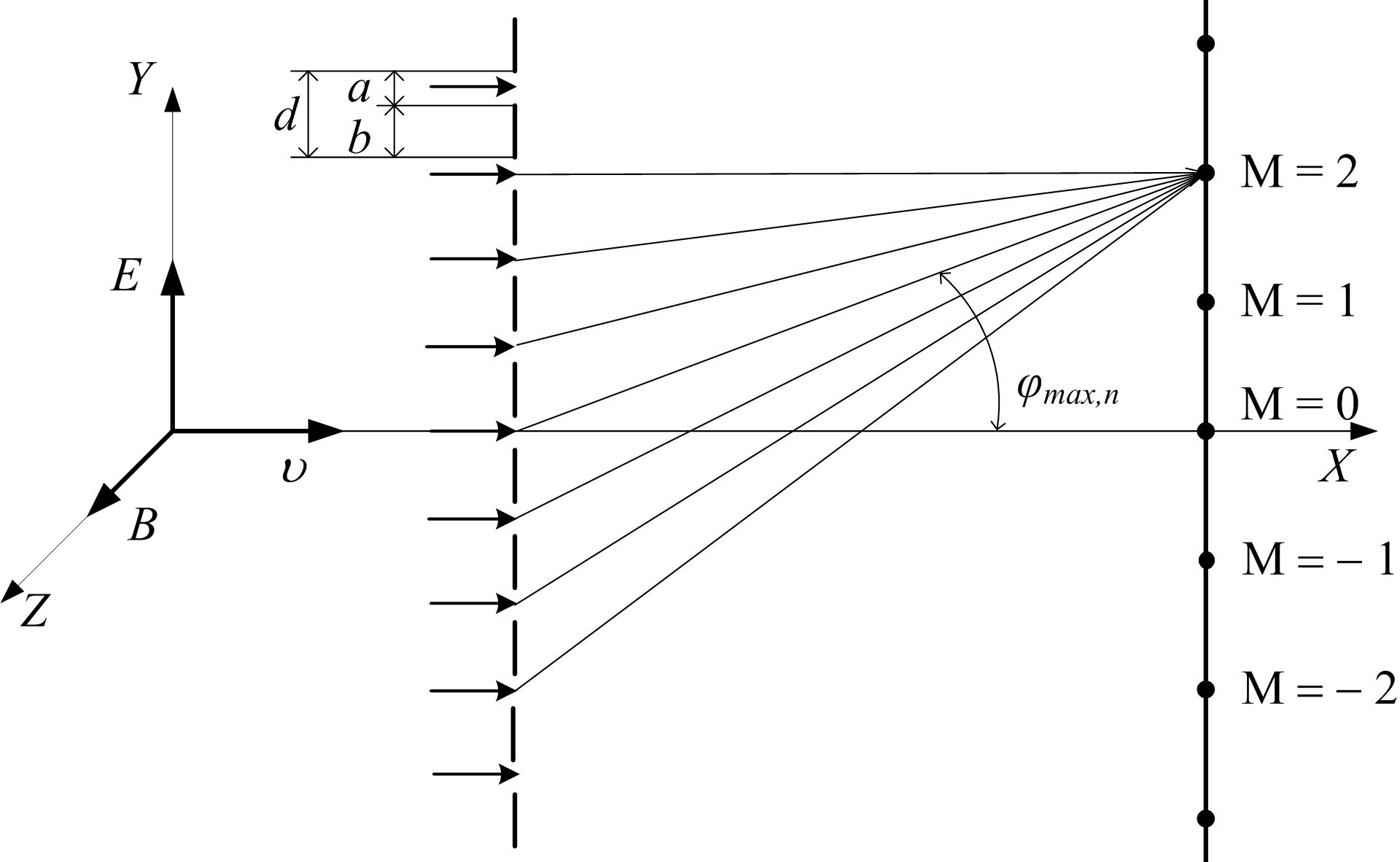
Рис. 2

Если волны, идущие от щелей, некогерентны, то вид дифракционной картины с увеличением числа щелей не изменится, но ее интенсивность в соответствии с законом сохранения энергии возрастет в N раз. В нашем опыте электромагнитные волны, идущие от лазерного источника, когерентны, щели не нарушают когерентности волн. Так как среда за щелями изотропна, то дифрагированные световые потоки, идущие от любых соседних щелей, также когерентны, и при сложении в достаточно удаленной точке пространства дадут устойчивую интерференцию. Таким образом, в пространстве за решеткой возникает дополнительное (по сравнению с одной щелью) перераспределение световых потоков, что приведет к появлению в дифракционной картине добавочных минимумов и так называемых главных максимумов, интенсивность которых возрастет в N² раз за счет интерференции. Условие образования главных максимумов и минимумов в дифракционной картине для любого числа щелей запишется в виде

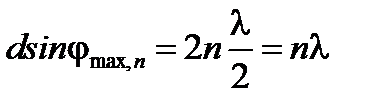, (4)

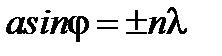, (4¢)

где n = 0; ±1; ± 2;... – целое число, определяющее порядок главных максимумов и минимумов; j – углы дифракции.

Между любыми двумя главными максимумами расположено (N - 1) добавочных минимумов, разделенных вторичными максимумами очень малой интенсивности. Условие образования в дифракционной картине от N щелей дополнительных минимумов запишется так:

Nd sin j _min,n = nl, (5)

где n — любое целое число, кроме N, 2N, 3N и т. д.

Распределение интенсивности в дифракционной картине от N щелей может быть выражено соотношением

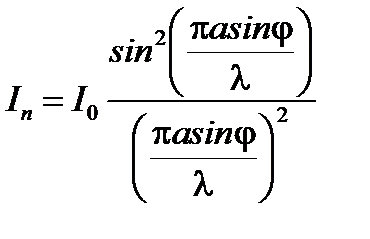
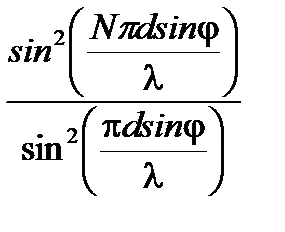, (6)

где I₀ – интенсивность световых колебаний определяемых одной щелью в направлении нормали.

Интенсивности главных максимумов различных порядков для а < b равны [3]

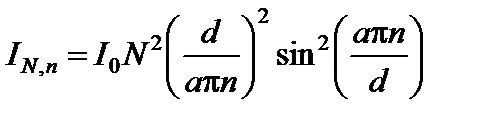, (7)

где I_N,0 = I₀N ² – интенсивность освещенности нулевого (главного) максимума.

Очевидно из формулы (7), что отношение I_N,n/I_N,0 зависит от величины а/d.

Из условий (4) – (7) так же следует, что самым интенсивным для любых длин волн является главный нулевой максимум, наблюдаемый в центре дифракционной картины под углом j₀ = 0 при n = 0, что физически соответствует сложению в фазе колебаний, происходящих в центре дифракционной картины.

Положение главных максимумов не зависит от числа щелей в решетке, но определяется длиной волны света и величиной периода решетки Расстояние между любыми соседними главными максимумами l = Ll/d и постоянно для заданных d, l и L [3]. Изменение ширины щелей а приведет не к изменению расстояния между главными максимумами, а к перераспределению интенсивности дифракционной картины (6). С увеличением числа щелей ширина главных максимумов уменьшается, а дифракционная картина, полученная от решетки с большим числом щелей, четче очерчена.

Так как положение дифракционных максимумов не зависит от материала решетки, а определяется величиной d и длиной волны l, то, получив экспериментально углы дифракции для этих максимумов, можно рассчитать соответствующие им длины волн по известному периоду d, либо определить d, зная спектральный состав падающего на решетку света.

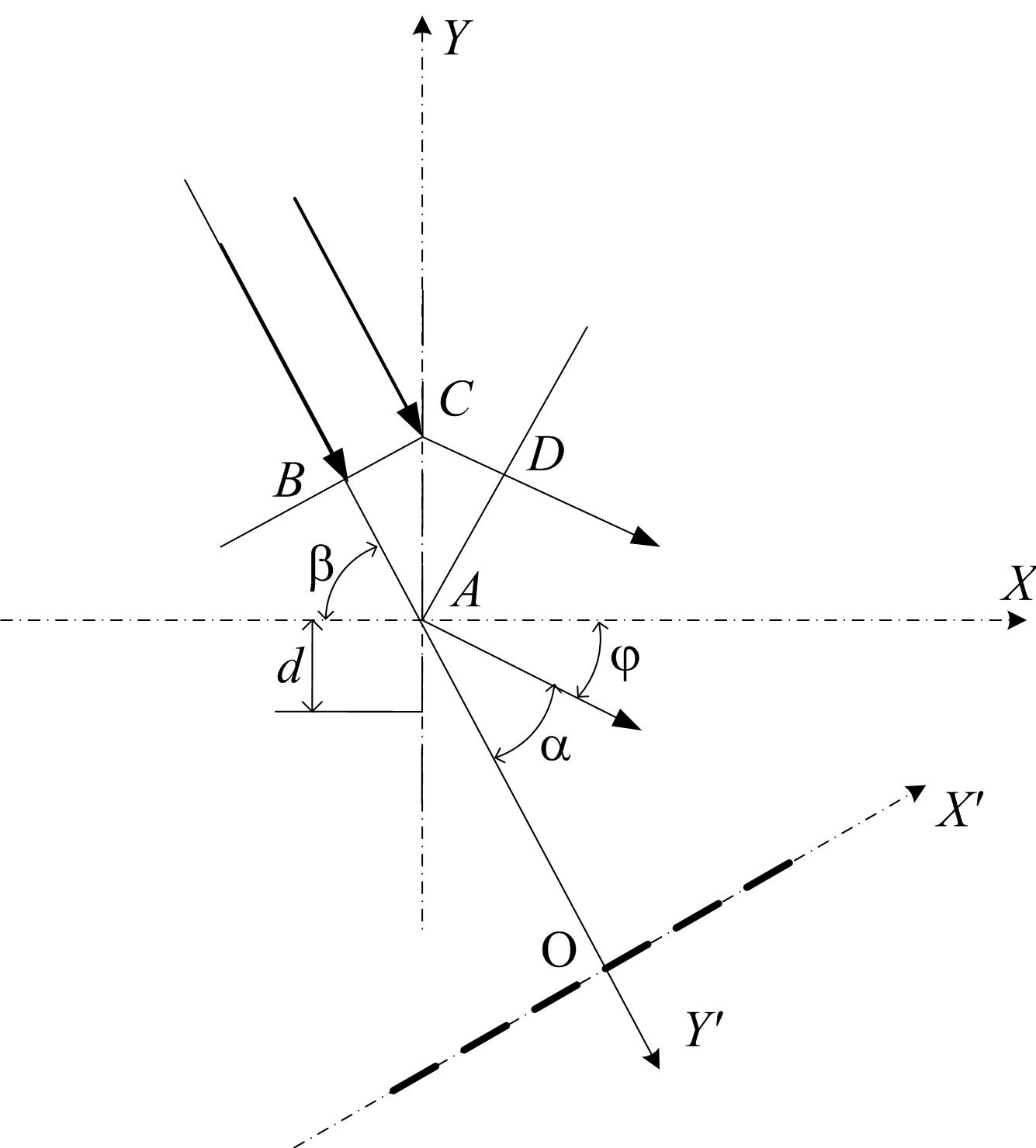
Рис. 3

Расстояния между соседними главными максимумами обратно пропорциональны периоду решетки, поэтому для грубых решеток при d соседние главные максимумы дифракционной картины близко расположены и могут быть не различены (не разрешены решеткой). Для увеличения разрешения решеткой соседних максимумов необходимо уменьшить период решетки; такая задача бывает технически трудновыполнима, и для увеличения разрешения используют косое фиксированное падение волн на решетку под углом b к нормали (рис 3).

Сравнение условий образования n-го максимума при косом падении света на решетку и нормальном падении показывает, что увеличение угла падения b дает тот же эффект, что и уменьшение периода решетки.

Если в опыте угол b можно выбрать близким к p/2, то эффективный период будет достаточно малым и расстояния между соседними главными максимумами увеличатся. Таким образом, на грубой решетке, используя косое падение волн, можно получить отчетливую дифракционную картину.

Следует добавить, что дифракционную картину можно наблюдать, поставив за дифракционной решеткой тонкую собирающую линзу. Экран для наблюдений помещают в фокальную плоскость линзы. Так как линза не вносит дополнительной разности хода (таутохронизм линзы), условия образования максимумов и минимумов освещенности в дифракционной картине записываются в прежнем виде (4), (5). Линза распределит падающий на ее поверхность световой поток по оптическому экрану в соответствии с углами падения световых волн по отношению к главной оптической оси линзы. Дифракционная картина приблизится к решетке, станет более четкой, расстояния между главными максимумами уменьшатся.