Приклади розв’язування задач. Задача 1. Із пункту А до пункту В, відстань між якими l =7,5км, одночасно назустріч один одному почали рухатися два велосипедиста: перший – зі швидкістю
Задача 1. Із пункту А до пункту В, відстань між якими l =7,5км, одночасно назустріч один одному почали рухатися два велосипедиста: перший – зі швидкістю 18км/год, другий – 9км/год. Визначити час, через який вони зустрінуться, і відстань від пункту А до місця зустрічі.
Розв’язання:
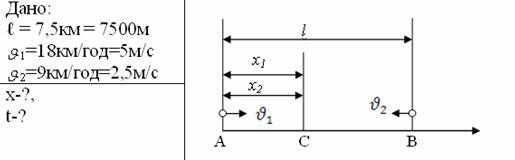
У момент зустрічі (точка С) координати велосипедистів будуть однакові. Запишемо рівняння руху велосипедистів, враховуючи, що у початковий момент (t=0) перший велосипедист знаходився на початку координат, а другий – у точці В, координату якої позначимо ?. Для велосипедиста, що рухається з пункту А: 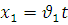 .
.
Для велосипедиста, що рухається з пункту В: 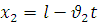 .
.
В момент зустрічі 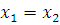 , тобто.
, тобто. 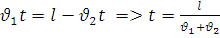
Місце зустрічі (координата точки С): 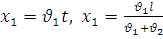 .
.
Підставивши числові значення, знайдемо значення величини:
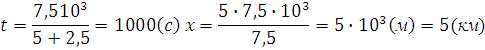
Відповідь: t =1000c, x = 5км.
Задача 2. Моторний човен першу половину шляху рухався по озеру зі сталою швидкістю 36км/год, а другу – зі швидкістю 18км/год. Чому дорівнює середня швидкість моторного човна на всьому шляху?
Розв’язання:
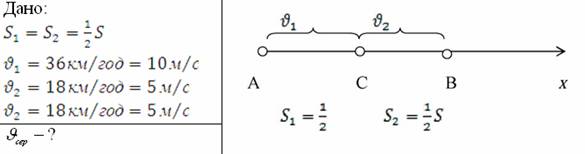
Середню швидкість човна на всьому шляху визначимо за формулою: 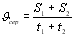 , для першої половини -
, для першої половини - 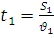 , для другої -
, для другої - 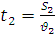 . Підставимо значення
. Підставимо значення 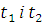 у формулу для
у формулу для 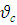 і, врахувавши
і, врахувавши 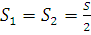 , отримаємо:
, отримаємо: 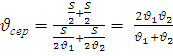 .
.
Зробивши обчислення, отримаємо: 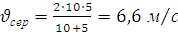 .
.
Відповідь: 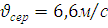 .
.
Задача 3. Моторний човен проходить відстань між двома пунктами А і В за течією річки протягом часу t1 = 3год, а пліт – протягом часу t = 12год. Скільки часу t2 витратить моторний човен на зворотний шлях?
Розв’язання:
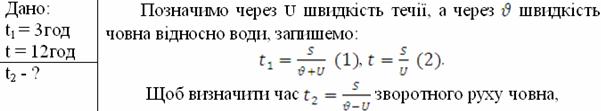
рівняння (1) і (2) запишемо так:
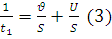
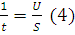
Віднімемо від рівняння (3) подвоєне рівняння (4), дістанемо:
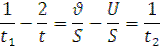
Звідки: 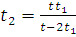 , підставимо числа, отримаємо:
, підставимо числа, отримаємо: 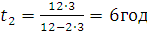 .
.
Відповідь: 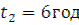
Дата добавления: 2015-09-11; просмотров: 5320;
