Рівномірний прямолінійний рух. Графіки залежності кінематичних величин від часу
Прямолінійним рівномірним рухом називається рух, за якого матеріальна точка, рухаючись по прямій, за будь-які рівні проміжки часу здійснює однакові переміщення. Це найпростіший вид механічного руху. Прикладом такого руху наближено можна вважати рух на прямолінійній ділянці стрічки транспортера, східців ескалатора, рух потягу в метро після розгону, рух парашутиста тощо.
Кінематичними характеристиками цього руху є: переміщення, швидкість, коорди-ната, шлях. Переміщенням називають вектор 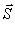 , що сполучає на траєкторії два послідовні положення рухомої матеріальної точки. Під час прямолінійного руху тільки в одному напрямі шлях і довжина вектора переміщення збігаються. В усіх інших випадках модуль переміщення менший за довжину шляху, що з плином часу завжди зростає.
, що сполучає на траєкторії два послідовні положення рухомої матеріальної точки. Під час прямолінійного руху тільки в одному напрямі шлях і довжина вектора переміщення збігаються. В усіх інших випадках модуль переміщення менший за довжину шляху, що з плином часу завжди зростає.
Швидкістю рівномірного прямолінійного руху називають векторну фізичну величину 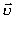 , що дорівнює відношенню вектора переміщення
, що дорівнює відношенню вектора переміщення 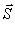 до проміжку часу, протягом якого це переміщення відбулося:
до проміжку часу, протягом якого це переміщення відбулося:

Напрям вектора швидкості в прямолінійному русі збігається з напрямом вектора переміщення. У рівномірному прямолінійному русі за будь-які однакові проміжки часу тіло виконує однакові переміщення, тому швидкість такого руху є величиною сталою ( 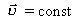 ). Оскільки у разі такого руху в одному напрямі переміщення чисельно дорівнює пройденного шляху s, то модуль швидкості
). Оскільки у разі такого руху в одному напрямі переміщення чисельно дорівнює пройденного шляху s, то модуль швидкості 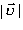 рівномірного прямолінійного руху
рівномірного прямолінійного руху
Одиниця швидкості в СІ – 1 м/с; 1 м/с – це швидкість такого рівномірного прямолі-нійного руху, за якого матеріальна точка за 1 с здійснює переміщення 1 м.
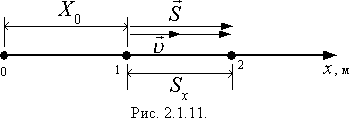
Нехай вісь Ох системи координат, пов'язаної з тілом відліку, збігається з прямою, вздовж якої рухається тіло, а X0 є координатою початкового положення тіла. Уздовж осі ОХ напрямлені і переміщення 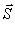 , і швидкість
, і швидкість 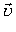 рухомого тіла (рис.2.1.11).
рухомого тіла (рис.2.1.11).
Із формули (2.1.2) знаходимо: 
Згідно із формулою (2.1.4) вектори 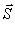 і
і 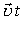 однакові, тому однаковими будуть і їх проекції на вісь Ох:
однакові, тому однаковими будуть і їх проекції на вісь Ох:

Тепер можна встановити кінематичний закон рівномірного прямолінійного руху, тобто знайти вираз для координати рухомого тіла в будь-який момент часу. Оскільки Х у точці 2 (рис.2.1.11) можна знайти за формулою
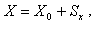
то з урахуванням рівняння (2.1.5) маємо:

Вираз (2.1.6) називають рівнянням рівномірного прямолінійного руху. За формулою (2.1.6), знаючи початкову координату X0 положення 1 (рис.2.1.11) тіла і його швидкість у будь-який момент часу, можна визначити положення рухомого тіла. Права части-на цієї формули – алгебраїчна сума, оскільки X0 і vx можуть бути додатними і від'ємними. Знак плюс відповідає руху в додатному напрямі осі Ох, знак мінус – у від'ємному.
Якщо тіло рівномірно рухається по прямій лінії в площині, то цей рух описується системою рівнянь:
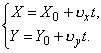
Під час прямолінійного рівномірного руху в просторі система набуде вигляду:
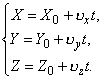
Під час прямолінійного руху уздовж координатної осі Ох шлях дорівнює зміні значень кінцевої і початкової координат, тобто 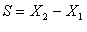 , тому модуль швидкості
, тому модуль швидкості 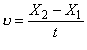 . Отже, швидкість прямолінійного рівномірного руху чисельно дорівнює зміні координати за одиницю часу. Вона показує, як швидко змінюється координата Х положення матеріальної точки.
. Отже, швидкість прямолінійного рівномірного руху чисельно дорівнює зміні координати за одиницю часу. Вона показує, як швидко змінюється координата Х положення матеріальної точки.
Із формули (2.1.3) одержують рівняння шляху прямолінійного рівномірного руху

Шлях, пройдений матеріальною точкою у разі прямолінійного рівномірного руху, прямо пропорційний часу руху і завжди зростає.
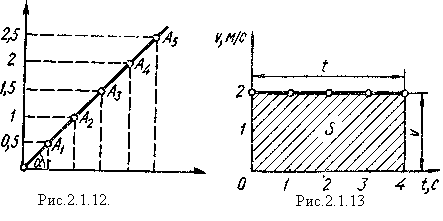
Функціональну залежність між кінематичними величинами можна виражати не тільки у вигляді рівнянь, але й графічно. Як приклад розглянемо графік шляху рівномірного руху (рис.2.1.12).
На рис.2.1.13 показано графік швидкості прямолінійного рівномірного руху (v = 2 м/с). За допомогою графіка швидкості можна визначити шлях, пройдений тілом за будь-який проміжок часу. Як видно з рис.2.1.13, шлях чисельно дорівнює площі прямокутника, одна сторона якого дорівнює швидкості, а друга –проміжку часу.
Нехай два тіла рухаються рівномірно вздовж осі Ох, одне – зі швидкістю v1 в додатному напрямі осі 2.1.6, друге – зі швидкістю v2 у від'ємному напрямі тієї ж осі. Тоді, vx1 >0, vx2 >0. На рис.2.1.14 для цих тіл зображено графіки залежностей проекцій швидкостей від часу. Ці графіки паралельні осі часу t; друге тіло рухається з більшою за модулем швидкістю і в протилежному напрямі.
На рис.2.1.15 показано графіки залежностей координат цих самих тіл від часу, тобто графіки залежностей вигляду 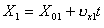 ,
,  ,
, 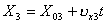 . З графіків видно, що
. З графіків видно, що 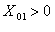 , а
, а 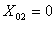 ,
, 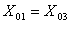 ,
, 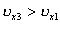 .
.
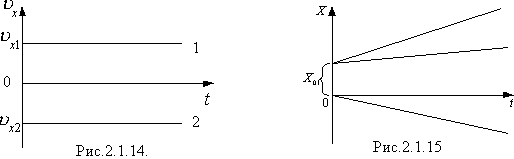
Дата добавления: 2015-09-11; просмотров: 3834;
