Приклади розв’язування задач
Задача 1. Літак у момент відривання від Землі має швидкість 240км/год і пробігає по бетонній доріжці відстань 790м. Скільки часу триває розбіг і з яким прискоренням рухався при цьому літак?
Розв’язання:

початкова швидкість - 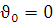 , тоді
, тоді 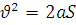 , звідки
, звідки
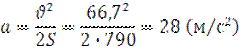
Для рівноприскореного руху 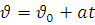 ,
, 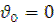 ,
, 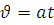
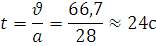
Відповідь: 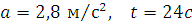 .
.
Задача 2. Вийшовши із стану спокою, тіло рухалося рівноприскорено протягом 4с, а потім наступні 6с стало рухатися рівномірно і пройшло 18м з тією швидкістю, якої воно набуло на кінець четвертої секунди. Визначити прискорення і шлях, пройдений тілом за весь час руху.
Розв’язання:

Шлях рівноприскореного руху 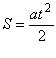 - , а шлях рівномірного руху -
- , а шлях рівномірного руху - 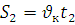 .
.
Врахувавши 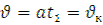 , отримаємо
, отримаємо 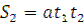 , звідки
, звідки
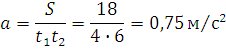
Шлях, який тіло пройшло за перші 4с, буде рівний 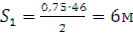 ,
,
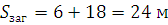
Відповідь: 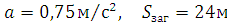 .
.
Задача 3. Переміщення тіла при рівноприскореному русі за перші два рівні послідовні інтервали часу по 2с кожен відповідно дорівнюють 12м і 32м. Знайти початкову швидкість і прискорення тіла.
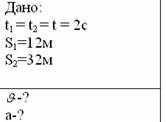 Розв’язання:
Розв’язання: 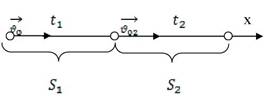
Кінцева швидкість, набута на проміжку 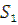 за час
за час 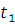 , буде початковою на проміжку S2:
, буде початковою на проміжку S2: 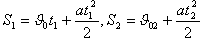
Врахувавши 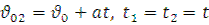 , отримаємо:
, отримаємо:
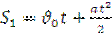 (1)
(1)
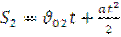 (2)
(2)
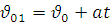 (3)
(3)
Підставивши (3) в (2) , отримаємо:
 .
.
Звідки: 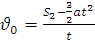 (4)
(4)
Тепер підставимо (4) в (1):
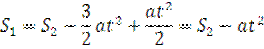
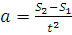 , тоді
, тоді 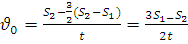
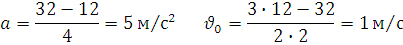
Відповідь:  .
.
Задача 4. Потяг відійшов від станції і протягом 15с рухався рівноприскорено. Знайти шлях, пройдений потягом за цей час, і швидкість його в кінці цього шляху, якщо відомо, що за 15-ту секунду потяг пройшов шлях на 2м більше, ніж за попередню.
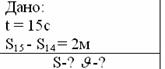
Розв’язання:
Рух рівномірний без початкової швидкості, тому пройдений шлях:
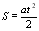
Врахувавши, що при рівноприскореному русі шляхи, що проходить тіло за рівні послідовні проміжки часу, відносяться один одного, як рядок послідовних непарних чисел, можна записати:
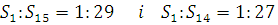 звідки
звідки 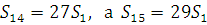
Врахувавши 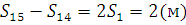 ,отримаємо:
,отримаємо: 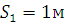

Підставивши числові значення прискорення 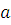 і часу t у формулу для шляху
і часу t у формулу для шляху 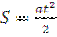 , отримаємо:
, отримаємо: 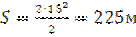 . Швидкість потягу в кінці 15-ї секунди обчислюється:
. Швидкість потягу в кінці 15-ї секунди обчислюється:
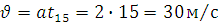
Відповідь: S=225м, 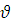 =30м/с
=30м/с
1.5. Вільне падіння
Рух тіла під дією тільки сили тяжіння називається вільним падінням.
Вільне падіння відбувається з прискоренням, яке називається прискоренням вільного падіння. При розв’язуванні задач прискорення вільного падіння поблизу поверхні Землі рівне 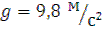 .
1. Якщо початкова швидкість дорівнює нулю (v0=0), то .
1. Якщо початкова швидкість дорівнює нулю (v0=0), то
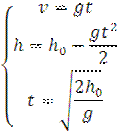 h0– початкова висота, t-час падіння, v- швидкість тіла у момент часу,
2. Початкова швидкість напрямлена вертикально вгору:
h0– початкова висота, t-час падіння, v- швидкість тіла у момент часу,
2. Початкова швидкість напрямлена вертикально вгору:
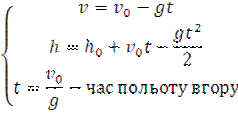 t =
t = 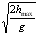 - час польоту вниз. - час польоту вниз.
 – максимальна висота, якої досягає тіло. Максимальна висота буде обраховуватися hmax = h0 + – максимальна висота, якої досягає тіло. Максимальна висота буде обраховуватися hmax = h0 + 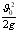 . .
|
Дата добавления: 2015-09-11; просмотров: 2926;
