Метод розкриття визначника за елементами рядка або стовпця
Означення. Мінором 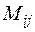 елемента
елемента 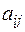 називається визначник (n-1)-ого порядку, який утворюється із заданого визначника n-го порядку викреслюванням i-ої строки та j -ого стовпця.
називається визначник (n-1)-ого порядку, який утворюється із заданого визначника n-го порядку викреслюванням i-ої строки та j -ого стовпця.
Означення. Алгебраїчним доповненням 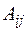 елемента
елемента 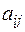 є добуток
є добуток
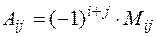 .
.
Зауваження. Таким чином, коли показник степеня 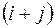 є парним, тоді значення мінора та алгебраїчного доповнення співпадають. Коли показник степеня
є парним, тоді значення мінора та алгебраїчного доповнення співпадають. Коли показник степеня 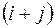 є непарним, тоді значення мінора та алгебраїчного доповнення є протилежними числами.
є непарним, тоді значення мінора та алгебраїчного доповнення є протилежними числами.
Приклади обчислення мінорів та алгебраїчних доповнень.
| Визначник | Мінор | Алгебраїчне доповнення |
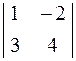
| 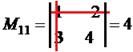
| 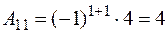
|
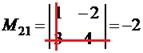
| 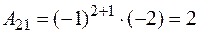
| |
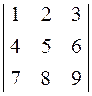
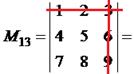
| 
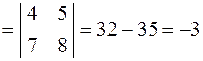
| 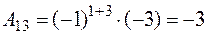
|
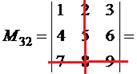
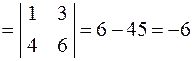
| 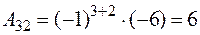
|
Теорема. Визначник порядку n дорівнює сумі добутків елементів будь-якого рядка (або стовпця) на їх алгебраїчні доповнення:
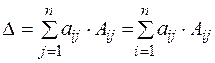 . .
| (1.2) |
Зауваження. Записана теорема є окремим випадком більш загальної теореми, яка доведена Лапласом у 1772 р. Окремий випадок теореми Лапласа зустрічається ще раніше у рукописах Лейбніца.
Теорема Лапласа. Нехай А — квадратна матриця розміру 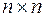 в якій вибрано довільні k рядків (стовпців). Тоді визначник матриці
в якій вибрано довільні k рядків (стовпців). Тоді визначник матриці 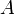 дорівнює сумі всіляких добутків мінорів
дорівнює сумі всіляких добутків мінорів 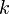 -го порядку, розташованих в цих рядках (стовпцях), на їх алгебраїчні доповнення:
-го порядку, розташованих в цих рядках (стовпцях), на їх алгебраїчні доповнення:
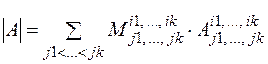 , ,
| (1.3) |
де підсумовування ведеться по всіх номерах стовпців (рядків) 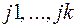 .
.
Число мінорів, по яких береться сума в теоремі Лапласа, рівне числу способів вибрати k стовпців з n, тобто біноміальному коефіцієнту 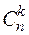 .
.
Приклад. Розкрити визначник із приклада 1 за елементами другого стовпця.
Розв’язання.
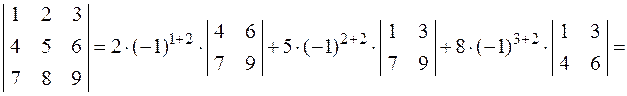
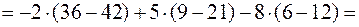
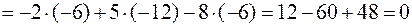 .
.
Дата добавления: 2015-09-11; просмотров: 1946;
