Математическое описание аэродинамической схемы замещения

В аэродинамической схеме замещения выполняются законы сохранения энергии. Согласно закону сохранения массы, сумма масс воздуха, подходящих к узлу в единицу времени, должна быть равна сумме масс, уходящих от узла в единицу времени. Поскольку удельный вес воздуха в районе узла практически не меняется, вместо масс можно рассматривать расход воздуха Q. Для i - го узла справедливо выражение

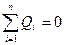, (1)

где n - количество ветвей схемы, подходящих к i - тому узлу. Выражение (1) является первым законом Кирхгофа для аэродинамической схемы замещения.

Закон сохранения энергии для i - того замкнутого контура схемы замещения записывается в виде

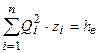, (2)

т.е. алгебраическая сумма падений напоров всех ветвей замкнутого контура равна напору воздуха 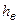, создаваемого вентилятором. Если в контуре вентилятора нет, то 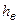принимается равным нулю.

Использование аэродинамических схем замещения с большим числом ветвей и контуров приводит к необходимости совместного решения системы уравнений. Для любой замкнутой схемы замещения, имеющей N узлов, М независимых контуров и L ветвей справедливо соотношение

,

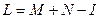Число независимых уравнений для узлов равно N -1, так как уравнение последнего узла вытекает из уравнений для всех предыдущих узлов. Общее число уравнений в системе будет М + N - I, т. е. L. Для решения системы уравнений используют численные методы и ЭВМ.

Падение напора 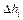на i-м аэродинамическом сопротивлении определяется по формуле:

при турбулентном режиме:

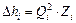(3) ;

при ламинарном режиме:

,

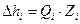где 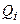- расход воздуха через i- й канал;

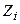- аэродинамическое сопротивление i- го канала.

В тяговом двигателе при независимой системе вентиляции имеем турбулентный режим движения охлаждающего воздуха, поэтому при составлении уравнения в соответствии с (2) для контура схемы замещения будет использоваться нелинейное выражение (3). В связи с этим математической моделью аэродинамической схемы замещения является система нелинейных алгебраических уравнений.