Непрерывные случайные величины.

Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал.

Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе.

Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей 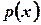. Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:

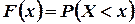
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее, чем х.

Формула (3.4) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.

Случайная величина 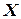называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция (функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода) 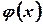, удовлетворяющая для любых значений xравенству

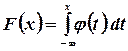(3.5)

Функция 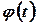называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если 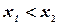, то на основании формул (3.3) и (3.4) имеем

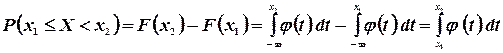(3.6)

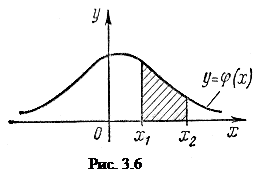
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств 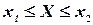равна площади криволинейной трапеции с основанием 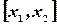, ограниченной сверху кривой 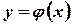(рис. 3.6).

Так как 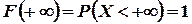, а на основании формулы (26) 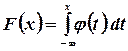, то

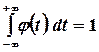(3.7)

Далее, пользуясь формулой (3.5), найдем 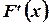, производную от 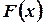, как производную от интеграла по переменной верхней границе, считая плотность распределения 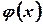непрерывной. Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,

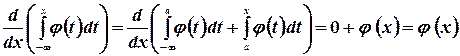
Так как интеграл 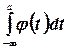есть величина постоянная. Таким образом

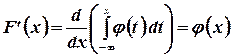(3.8)

Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция 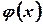непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.

Далее, на основании формулы (3.6), полагая 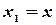, , 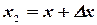имеем:

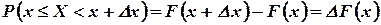
В силу непрерывности функции F(х) получим, что 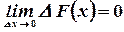. Следовательно 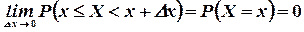. Таким образом,