Перевод дробных чисел

Если при переводе конечной дроби в другую систему счисления получается конечная дробь, то такой перевод называется точным. Если при переводе получается бесконечная дробь, тогда перевод называется приближенным.

Перевод дробных чисел из n-й в десятичную систему счисления - вещественное число переводится из n-й в десятичную систему счисления с использованием формализованного представления числа.

Перевод дробных чисел с нулевой целой частью из десятичной в n-ую систему счисления - дробное число X, у которого целая часть равна 0, переводится из десятичной в n-ую систему счисления по следующему алгоритму:

1) умножить X на n;

2) получить цифру как целую часть числа X и приписать ее справа от имеющихся цифр;

3) обнулить целую часть числа X;

4) выполнять шаги 1-3, пока X ¹ 0 (при точном переводе) или до получения нужного количества цифр в дробной части (при приближенном переводе с заданной точностью).

Пример. Перевести число 0,6875 в двоичную систему счисления.

Решение. Вновь схему перевода запишем в виде столбца.

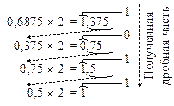
На последнем шаге перевода получена единица. После обнуления целой части получим 0. Значит, перевод закончен. Результат перевода числа 0,6875 в двоичную систему счисления – число 0,1011₂.

Если бы нам было необходимо получить дробную часть с точностью до 3 знаков, то процесс перевода был бы остановлен после получения 3 цифр в дробной части. □

Перевод дробных чисел с ненулевой целой частью из десятичной в n-ую систему счисления - при переводе дробных чисел из десятичной в n-ую систему счисления отдельно переводятся целая и дробная части.

Десятичная система счисления может использоваться в качестве промежуточного этапа при переводе чисел из одной системы счисления в другую. Приведенные в этой главе правила позволяют перевести числа из одной системы счисления в десятичную, а из нее – в любую другую системы счисления

Логические основы ЭВМ

Принципы работы ЭВМ основываются на законах математической логики, поэтому ее элементы широко используются для поиска и обработки информации и при разработке схем электронных устройств.

Математическая логика – это наука о формах и способах мышления и их математическом представлении.

Высказывание - повествовательное предложение, относительно которого определенно и объективно можно сказать истинно оно или ложно (ЛОЖЬ или ИСТИНА, 0 или 1, TRUE или FALSE).

Алгебра логики – раздел математики, изучающий процессы умозаключений и законы, которые позволяют из истинности одних высказываний делать заключения об истинности или ложности других высказываний, независимо от их конкретного содержания.

Умозаключение позволяет из известных фактов (истинных высказываний) получать новые факты. Например, из факта «Все углы треугольника равны» следует истинность высказывания «Этот треугольник равносторонний».

Алгебра логики (булева алгебра) была создана в 1854 г. Дж. Булем и в настоящее время находит широкое применение при разработке алгоритмов и для структурно-функционального описания, анализа и синтеза современных электронных схем.