Перший постулат Бора.
Електрон в атомі може обертатися лише по тих орбітах, на яких коловий момент руху 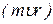 є цілим числом, кратним сталій Планка, поділеній на
є цілим числом, кратним сталій Планка, поділеній на  :
:

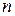 – 1, 2, 3,…,∞
– 1, 2, 3,…,∞
Такі орбіти – стаціонарні. Під час руху електрона по стаціонарній орбіті він не випромінює електромагнітної енергії.
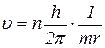 підставимо в рівняння сталості орбіт:
підставимо в рівняння сталості орбіт:
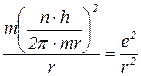
Тоді радіус електронних орбіт в атомі гідрогену:
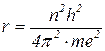
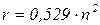
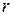 виражається в Ả (1 Ả =
виражається в Ả (1 Ả = 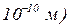 .
.
Енергія орбіти
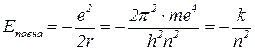
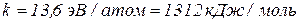 .
.
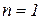 – основний стан;
– основний стан;
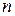 > 1 – збуджений стан.
> 1 – збуджений стан.
У разі поглинання енергії атомом маленькими порціями (квантами) відбувається стрибкоподібне переміщення електрона по стаціонарних орбітах від ядра атома. Зворотній перебіг супроводжується виділенням енергії.
Умови переміщення електрона з одного квантового рівня на інший визначає другий постулат Бора:
Під час стрибкоподібного переходу електрона з більш віддаленого квантового рівня на ближчу до ядра орбіту атом випромінює квант енергії з певною частотою коливань 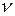 :
:
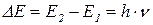
Хвильовий характер електрона.
Згідно з теорією Бора електрон розглядали як класичну частинку, і тому її рух описували законами класичної механіки та електродинаміки. У 1924 р. де Бройль запропонував поняття "корпускулярні хвилі" та висловив ідею про хвильову природу електрона.
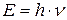 ;
;
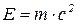 ;
;
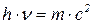 ;
; 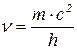 ;
; 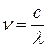 ;
;
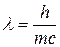
Для матеріальних частинок, подібних до електрона, які рухаються зі швидкістю 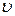 , цей вираз набуває вигляду:
, цей вираз набуває вигляду:
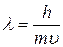
Гіпотеза де Бройля має загальний характер, і тому якому завгодно тілу масою 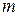 , що рухається зі швидкістю
, що рухається зі швидкістю 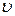 , має відповідати матеріальна хвиля. Довжина хвилі для макротіл, скажімо, тенісного м’яча, є настільки малою, що її неможливо виміряти за допомогою приладів. Для електронів же маса
, має відповідати матеріальна хвиля. Довжина хвилі для макротіл, скажімо, тенісного м’яча, є настільки малою, що її неможливо виміряти за допомогою приладів. Для електронів же маса 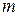 є набагато порядків меншою, тому величини
є набагато порядків меншою, тому величини 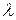 набувають вимірних значень.
набувають вимірних значень.
При розсіянні електронів кристалами спостерігається дифракція, подібна до дифракції рентгенівських променів. Це підтвердило припущення де Бройля про те, що електрону притаманні хвильові властивості: довжина хвилі, частота, фаза та здатність до інтерференції. Це припущення йде всупереч теорії Томсона про те, що електрон є частинкою з певною масою, енергією та моментом кількості руху.
Принцип додатковості Бора: електрон не може одночасно мати хвильові та корпускулярні властивості. Але для описання реальної поведінки електрона необхідно враховувати всі ці властивості, які взаємно доповнюють одне одного.
Відмінність у поведінці частинок мікросвіту та макротіл полягає в тому, що всі макротіла мають певне місце локалізації, тоді як стосовно мікрочастинок з їх двоїстою природою важко говорити про точну локалізацію. Хвиля як єдине ціле розподілена в просторі, і тому її положення неможливо точно визначити.
Принцип невизначеності Гейзенберга (обмеження точності, з якою можна визначити положення 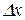 та імпульс
та імпульс 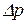 будь-якої мікрочастинки):
будь-якої мікрочастинки):
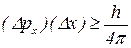
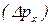 – невизначеність у величині імпульсу;
– невизначеність у величині імпульсу;
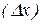 – невизначеність у положенні частинки у просторі.
– невизначеність у положенні частинки у просторі.
Таким чином, чим точніше виміряти імпульс, тим менш точно можна встановити положення в просторі.
Відповідно принципу невизначеності, електрон не можна уявляти як частинку, яка рухається від точки до точки, з певним імпульсом в кожній точці простору. Має сенс говорити тільки про деяку ймовірність перебування електрона у фіксованій точці простору. Не можна здійснити одночасне вимірювання з високою точністю таких фізичних величин, що дають можливість установити, є електрон матеріальною частинкою чи хвилею.
Рівняння Шредінгера (описує хвильовий рух електрона в атомі).
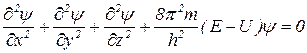
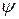 – хвильова функція;
– хвильова функція;
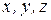 – координати;
– координати;
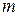 – маса електрона;
– маса електрона;
 – стала Планка;
– стала Планка;
 – повна енергія електрона;
– повна енергія електрона;
 – потенційна енергія електрона.
– потенційна енергія електрона.
Змінна величина 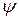 – хвильова функція. Вона є функцією координат, за якою можна знайти ймовірність. Вона пов’язана з амплітудою коливального руху електрона і може набувати як додатних, так і від’ємних значень, тоді як ймовірність завжди виражається додатним числом. Для розрахунків ймовірності знаходження електрона в певному місці використовують
– хвильова функція. Вона є функцією координат, за якою можна знайти ймовірність. Вона пов’язана з амплітудою коливального руху електрона і може набувати як додатних, так і від’ємних значень, тоді як ймовірність завжди виражається додатним числом. Для розрахунків ймовірності знаходження електрона в певному місці використовують 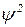 . Фізичний зміст
. Фізичний зміст 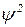 : добуток
: добуток  відповідає ймовірності перебування частинки в певному об’ємі
відповідає ймовірності перебування частинки в певному об’ємі 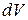 і має назву (для електрона) електронної густини.
і має назву (для електрона) електронної густини.
Хвильова функція має бути:
ü скінченною (не перетворюватись на ∞);
ü безперервною;
ü однозначною;
ü перетворюватись на 0 у разі нескінченного віддалення електрона від ядра.
Повне квантово-механічне розв’язання задачі про електронну будову атома 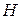 дає ряд хвильових функцій і відповідних їм енергій.
дає ряд хвильових функцій і відповідних їм енергій.
Стаціонарному стану електрона відповідає тільки одна дозволена комбінація трьох квантових чисел (цілочислові величини, за допомогою яких можна знайти кожну з виділених для розв’язання хвильових функцій) 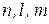 . Кожній такій комбінації відповідає один із розв’язків хвильового рівняння Шредінгера, який і називають хвильовою функцією, орбіталлю або електронною хмарою.
. Кожній такій комбінації відповідає один із розв’язків хвильового рівняння Шредінгера, який і називають хвильовою функцією, орбіталлю або електронною хмарою.
Орбіталь цілком визначена, якщо для неї відомі значення квантових чисел 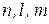 , цей набір є "адресою" електрона в атомі.
, цей набір є "адресою" електрона в атомі.
Дата добавления: 2015-09-02; просмотров: 1021;
