Уравнение состояния идеального газа

Уравнение состояния идеальногогаза устанавливает зависимость между основными термодинамическими параметрами (давление р, температура Т, удельный объем )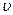

Идеальным газомназывается газ, в котором отсутствуют силы межмолекулярного взаимодействия, а объем молекул пренебрежимо мал. Важно, что при малом давлении (близком к атмосферному давлению) реальные газы с небольшой погрешностью можно считать идеальными газами.

Уравнение состояния идеального газа в 1834 г. установил французский физик Клапейрон.

Для 1 кг вещества уравнение Клапейрона имеет вид:

,

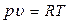где R – удельная газовая постоянная, .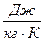

Удельная газовая постоянная R зависит от природы вещества и для разных газов она различна.

Для массы вещества М уравнение Клапейрона имеет вид:

,

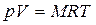где V – объем вещества, м³ , V = 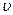М;

M – масса вещества, кг.

В 1874 г. русский ученный Менделеев применил уравнение Клапейрона к 1 киломолю вещества и получил универсальное уравнение состояния идеального газа, которое называется уравнением Менделеева-Клапейрона:

,

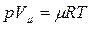где 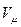- объем киломоля, ;

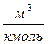μR – универсальная газовая постоянная, ;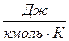

Универсальная газовая постоянная μR (в некоторых учебниках она обозначается Rμ) не зависит от природы вещества и для всех газов одинакова:

μR = 8314 .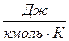

Существует однозначная взаимосвязь между универсальной газовой постоянной μR и удельной газовой постоянной вещества R, :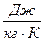

,

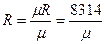где 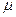- масса киломоля вещества, .

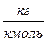В технике широко применяется приведение газа или пара к определенным условиям. Для получения этих соотношений используем уравнение Клапейрона в виде

.

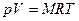Разделим переменные и постоянные величины:

.

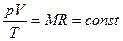Следовательно, для любых состояний газа (при М=const) будет выполняться равенство соотношений:

.

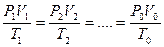Пример. Определить во сколько раз измениться объем газа при нагреве от 20°C до 900°C, если давление и масса газа останутся неизменными.

Решение:

;

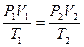откуда:

.

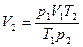Учитывая, что р₁ =р₂ получим:

.

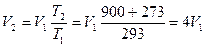Ответ: объем газа при нагреве от 20°C до 900°C увеличится в 4 раза.