Теоретические упражнения
1. Исходя из определения производной, доказать, что
a. а) производная периодической дифференцируемой функции есть функция периодическая;
b. б) производная четной дифференцируемой функции есть функция нечетная;
c. в) производная нечетной дифференцируемой функции есть функция четная.
2. Доказать, что если функция 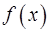 дифференцируема в точке
дифференцируема в точке 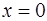 и
и 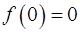 , то
, то 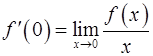 .
.
3. Доказать, что производная  не существует, если
не существует, если
4. 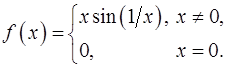
5. Доказать, что производная от функции
6. 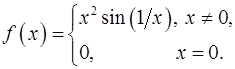
7. разрывна в точке 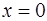 .
.
8. Доказать приближенную формулу
a. 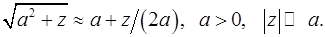
9. Что можно сказать о дифференцируемости суммы 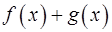 в точке
в точке  если, в этой точке:
если, в этой точке:
10. а) функция 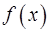 дифференцируема, а функция
дифференцируема, а функция 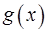 не дифференцируема;
не дифференцируема;
11. б) обе функции 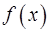 и
и 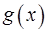 не дифференцируемы.
не дифференцируемы.
12. Пусть функция 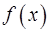 дифференцируема в точке
дифференцируема в точке 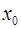 и
и  , а функция
, а функция 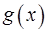 не дифференцируема в этой точке. Доказать, что произведение
не дифференцируема в этой точке. Доказать, что произведение 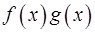 является недифференцируемым в точке
является недифференцируемым в точке 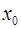 .
.
13. Что можно сказать о дифференцируемости произведения 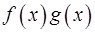 в предположениях задачи?
в предположениях задачи?
a. Рассмотреть примеры:
b. а) 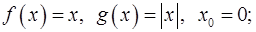
c. 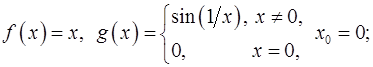
d. б) 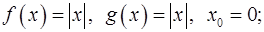
e. 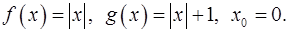
14. Найти  , если
, если 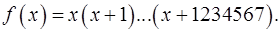
15. Выразить дифференциал 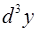 от сложной функции
от сложной функции 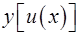 через производные от функции
через производные от функции  и дифференциалы от функции
и дифференциалы от функции 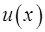 .
.
16. Пусть 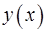 и
и 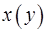 дважды дифференцируемые взаимно обратные функции. Выразить
дважды дифференцируемые взаимно обратные функции. Выразить 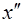 через
через 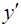 и
и 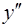 .
.
Дата добавления: 2015-09-11; просмотров: 913;
