Теоретические упражнения. У к а з а н и е. Доказать и использовать неравенство

1. Доказать, что если , то . Вытекает ли из существования 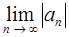существование ?

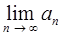У к а з а н и е. Доказать и использовать неравенство

.

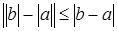2. Доказать, что последовательность расходиться.

3. Сформулировать на языке « 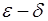» утверждение: «Число 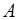не является пределом в точке 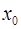функции 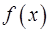, определенной в окрестности точки ».

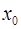4. Доказать, что если 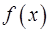непрерывная функция, есь также непрерывная функция. Верно ли обратное утверждение?

5. Сформулировать на языке « 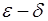» утверждение: «Функция 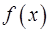, определенная в окрестности точки 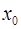, не является непрерывной в этой точке».

6. Пусть , а 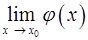не существует. Доказать, что не существует.

У к а з а н и е. Допустить противное и использовать теорему о пределе частного.

7. Пусть функция 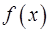имеет предел в точке 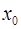, а функция 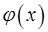не имеет предела. Будут ли существовать пределы:

1) 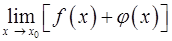; 2) ?

Рассмотреть пример: .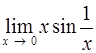

8. Пусть , а функция 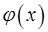бесконечно большая при 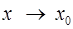. Доказать, что произведение 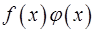является бесконечно большой функцией при .

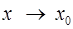9. Является ли бесконечно большой при 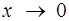функция ?

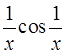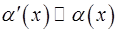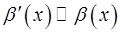10. Пусть и при 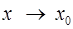. Доказать, что если 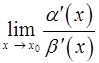не существует, то 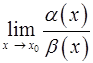тоже не существует.