Расчёт параметров сетевого графика табличным методом

В контрольной работе рекомендуется использовать табличный метод расчета параметров сетевого графика.

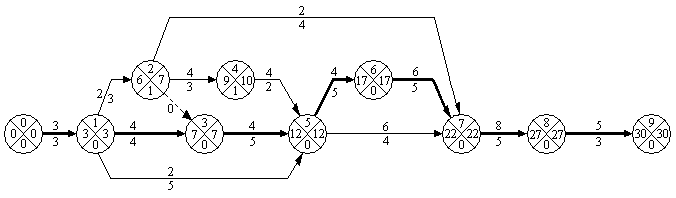
Рис. 16 - Сетевой график опытно-конструкторских работ по созданию нового образца рыбопромыслового оборудования для расчета табличным методом

Табличный метод расчёта параметров сетевого графика предусматривает расчёт параметров в таблице 2:

Таблица 4

Расчёт параметров сетевого графика табличным методом

Код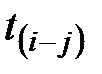
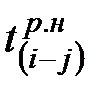
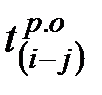
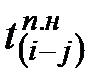
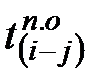
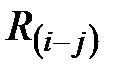
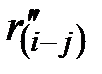
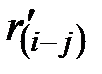
i	j

Расчёт параметров сетевого графика начинают с заполнения первых трёх граф таблицы.

В гр.1 и 2 записывают коды событий, строго по их возрастанию, а в гр.3 проставляют продолжительность выполнения работ.

Далее рассчитывают наиболее ранние сроки начала и окончания работ (см. табл.2, гр.4 и 5). Расчёт ведётся сверху вниз.

Для работ, опирающихся на исходное событие, наиболее раннее начало принимают равным нулю ( 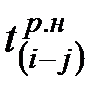) = 0 и проставляют в гр.4 табл.2.

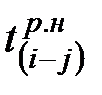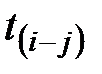Ранний срок окончания работ получается в результате сложения и в каждой строке

.

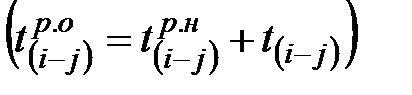Полученный результат записывают в гр.5 табл.2.

Для определения раннего срока начала последующих работ в вышерасположенных строках таблицы находится обозначение работы, у которой последующее событие j имеет номер предыдущего события i рассчитываемой работы, и значение 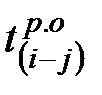из этой строки (гр.5) переносят в гр.4 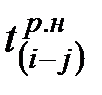строки рассчитываемой работы.

Если начальному событию рассматриваемой работы предшествует несколько работ, то в качестве 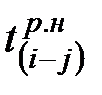выбирают наибольшее значение

.

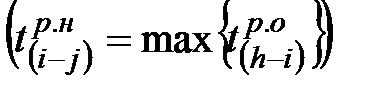Например, 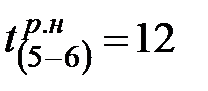, так как работе (5-6) предшествует три работы: (1-5), (3-5), (4-5), из которых работа (3-5) имеет максимальное раннее окончание равное 12, а работы (1-5) и (4-5) соответственно имеют 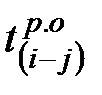, равное 8 и 11.

Расчёт наиболее поздних сроков начала и окончания работ ведётся снизу вверх в гр.6 и 7 табл.2.

Для завершающего события наиболее ранний срок свершения равен наиболее позднему сроку и равен продолжительности критического пути, т.е. .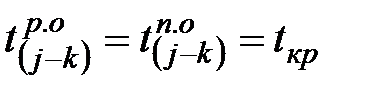

Для нашего случая .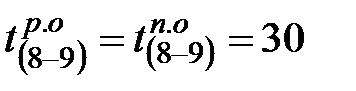

Это значение записываются в гр.7 табл.2.

Позднее начало определяется как разность между 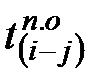и её продолжительностью, т.е. .

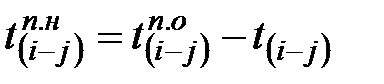Позднее окончание для каждой работы (i – j) определяется путём отыскания поздних начал работ - последующих за данной работой.

Если за ней следует одна работа, то 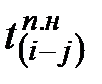будет являться 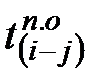для рассматриваемой работы и её значение из гр.6 переносят в гр.7 табл.6.2.

Например, данная работа (5-7), за ней следует одна работа (7-8), у которой 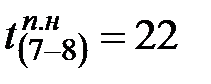, следовательно, .

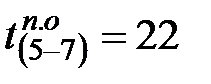Если за данной работой следует несколько работ, тогда выбирается минимальное значение позднего их начала.

Например, за работой (4-5) следуют две работы (5-6) и (5-7), т.е. 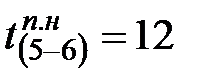и .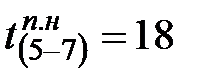

Выбирают минимальное значение, равное 12, и переносят из гр.6 в гр.7 для работы (4-5), т.е. .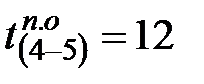

Полный (общий) резерв времени работы (i – j) определяют как разность между наиболее поздним (гр.7) и наиболее ранним (гр.5) окончанием работы (i – j), а результат записывают в гр.8 табл.2.

Например, .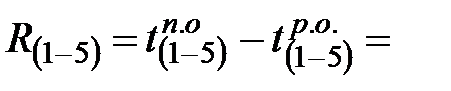

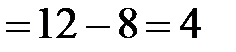Расчёт частных резервов времени работы (i – j) ведётся в табличной форме снизу вверх с использованием формул для определения частного резерва времени первого вида(результат записывают в гр.10 табл.2)

.

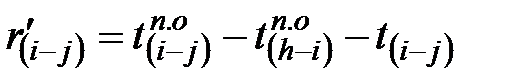Например, .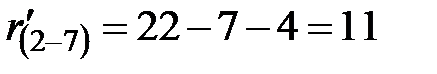

Частный резерв времени второго вида рассчитывается по формуле (результат заносят в гр.9 табл.2)

.

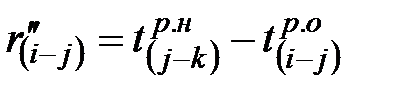Например, .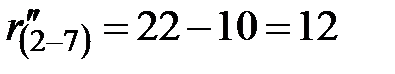

Важнейшим параметром любого сетевого гра­фика является критический путь.

Путемв сетевом графике называет­ся всякая последовательность работ (стрелок), связывающая между собой несколько событий. Путь, соединяющий исходное и заверша­ющее событие сети, считается полным, а все другие — неполными. Каждый путь характеризуется своей продолжительностью, которая равняется сумме длительностей составляющих его работ.

Полный путь, имеющий наибольшую продолжительность, называется крити­ческим путем. Стало быть, критический путь — это наиболее протя­женная по времени последовательная цепочка работ, ведущих от ис­ходного к завершающему событию. На сетевом графике (рис. 1) критический путь проходит через цепочку событий и работ, обозна­ченных номерами 0 - … - 9, и равен 30 дням. Он выделен жирной линией.

Работы и события, лежащие на критическом пути, принято также называть критическими. Полная продолжительность всего комплек­са работ, отображенных на сетевом графике, принимается всегда рав­ной критическому пути. Изменение продолжительности любой ра­боты, проходящей через критический путь, соответствующим обра­зом сокращает или удлиняет не только время выполнения промежу­точного события, но и всего срока наступления завершающего (ко­нечного) события, т.е. планируемые сроки осуществления проекти­руемых работ. Поэтому расчетные показатели, характеризующие про­должительность критических работ, а также экономические возмож­ности, которые открываются экономистам-менеджерам при исполь­зовании планово-управленческих решений, в значительной мере определяют и всю эффективность систем и методов сетевого планиро­вания.

В сетевых графиках имеется еще много других полных путей, ко­торые могут либо полностью, либо частично совпадать с критичес­ким путем, а также проходить вне критического пути. Поэтому в се­тевом планировании принято выделять напряженные и ненапряжен­ные пути. Напряженный путь — это критический путь. Ненапряжен­ныепути — это полные пути сетевого графика, которые по своей про­должительности меньше критического пути. Ненапряженные пути имеют на участках, не совпадающих с критическими работами, ре­зервы времени свершения событий. Это значит, что задержка в вы­полнении тех событий, которые не проходят через критический путь, до определенного этими резервами времени не будет оказывать вли­яния на расчетные или плановые сроки завершения всего проекта работ. Критические пути такими резервами времени не располагают. Это означает, если расчетное время свершения какого-либо события, находящегося на критическом пути, будет задержано, то этим самым будут отодвинуты на этот же период планируемые сроки наступления завершающего события.