ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДОВ АНАЛИЗА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Составление математической модели — это один из важных этапов исследования СИ.
Математические модели в зависимости от степени идеализации и преследуемых целей (гл. 3, 4) могут быть самыми различными как по виду уравнений, так и по их сложности. Возможность представления динамических свойств СИ во временной, частотной и комплексной областях разнообразит типаж их описаний. А необходимость решения таких задач, как определение статических и динамических характеристик или погрешностей, исследование вопросов преобразования квазидетерминированных и случайных сигналов, определение информационных характеристик, согласование сопротивлений и т. д., увеличивает разнообразие математических моделей разрабатываемых СИ.
Поэтому для решения многоплановых задач необходим достаточно разнообразный математический аппарат анализа математических моделей СИ.
Так, в соответствии с динамическими характеристиками, а также разновидностями описания динамических свойств СИ (гл. 3) можно выделить следующие наиболее часто применяемые подходы к исследованию математических моделей.
Во-первых, можно основываться на характере протекания процессов преобразования сигналов во времени и для формирования показателей качества СИ использовать, например, переходную или импульсную характеристику.
Во-вторых, можно исходить из частотных свойств СИ, характеризующих его поведение в установившемся режиме при действии на входе гармонического сигнала. Следует заметить, что оба эти подхода получили в настоящее время большое распространение и используются параллельно. Их выбор определяется удобством применения для СИ конкретного вида, а также сложившимися традициями в данной области приборостроения.
В-третьих, следует выделить обширный класс методов, например [11, 18, 19], корреляционного и спектрального анализа преобразования случайных сигналов в измерительных цепях. При этом представление статистических характеристик также возможно как во временной, так и в частотной областях.
И наконец, в настоящее время все чаще возникает необходимость [5] определения информационных характеристик СИ. Эти методы исследования основываются на использовании теории вероятностей.
Наиболее общей математической моделью является дифференциальное уравнение, поскольку передаточная функция, частотная статическая характеристики и т. д. могут быть получены из него путем соответствующих преобразований.
Уравнения, описывающие динамические свойства СИ, могут относиться к одному из классов: линейные дифференциальные уравнения с постоянными коэффициентами; линейные дифференциальные уравнения с переменными коэффициентами; нелинейные уравнения; дифференциальные уравнения в частных производных; разностные уравнения. Для каждого из этих классов имеются определенные методы анализа с представлением результата во временной, комплексной или частотной областях.
Прямой путь нахождения зависимости между выходным и входным сигналами во временной области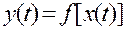 
— решение одного или системы дифференциальных уравнений. Если систему уравнений аналитически разрешить не удается, то, по крайней мере, необходимо найти те характеристики СИ, определение которых является одной из основных задач в процессе их исследования и разработки. При этом, например если определена переходная или импульсная характеристика, то при помощи интеграла свертки может быть найдена также зависимость .
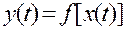Методы решения дифференциальных уравнений, а следовательно, и анализа математических моделей можно условно разделить на точные, приближенные и численные.
К точным относятся методы, позволяющие выразить решение через элементарные или специальные функции. Для решения линейных дифференциальных уравнений широко используют классический метод и преобразования Лапласа или Карсона — Хевисайда. Однако в связи со сложностью и громоздкостью применение этих методов ограничивается использованием уравнений сравнительно невысокого порядка.
Для анализа сложных математических моделей все большее распространение получают численные методы Эйлера, Рунге — Кутта. Адамса, ускоренной сходимости и др. Численные методы — это алгоритмы вычисления значений искомого решения у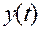 
на некоторой выбранной сетке аргумента. Решение при этом имеет вид таблицы. Численные методы не позволяют найти общего решения, но зато они применимы к очень широким классам уравнений. С появлением быстродействующих ЭВМ численные методы стали одними из основных для решения задач анализа математической модели СИ. Они являются практически единственным методом анализа, используемым в системах автоматизированного проектирования [1, 2].
Приближенными называются методы, при которых решение получается как предел некоторой последовательности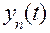 
, выраженной через элементарные функции. Если ограничиться конечным числом п, получим приближенное выражение для 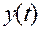. К приближенным относят обширный, часто используемый на практике, класс методов линеаризации, или упрощения, и идеализации модели с целью приведения ее к линейной и виду, для которого возможно применение точных методов. Примерами могут быть метод последовательных приближений, разложение в степенной ряд и др. Приближенные методы находят широкое применение для линеаризации и отыскания решения нелинейных уравнений.
Частотные методы анализа математической модели довольно хорошо разработаны и широко используются в теории автоматического управления. Это, например, критерии устойчивости Михайлова, Найквиста, логарифмических амплитудно-фазочастотных характеристик или частотных динамических характеристик. К ним относят полосу пропускания частот, граничную частоту и др., определение которых связано с допустимой частотной погрешностью. Поэтому определение амплитудно-фазочастотной характеристики и на ее основании частных динамических характеристик и составляет предмет анализа математической модели в частотной области.
Точных методов анализа нелинейных уравнений математической модели, позволяющих получить общее решение, не существует, за исключением метода припасовывания.Поэтому в процессе разработки СИ стремятся исключить нелинейности или, где это допустимо, выполняется линеаризация уравнений и задача сводится к анализу линейных уравнений. В частности, метод припасовывания [11] также предполагает разделение процесса на интервалы (участки), которые могут быть описаны линейными уравнениями. «Сшивание», или припасовывание, получаемых решений линейных уравнений и дает общее решение.
И наконец, в общем случае могут быть использованы приближенные и численные методы решения уравнений. Кроме того, для оценки устойчивости нелинейных СИ можно также воспользоваться известными в теории автоматического управления методами фазовых траекторий, точечных преобразований Ляпунова и др.
Методы анализа математических моделей СИ с распределенными параметрами, которые, как правило, представлены уравнениями в частных производных, базируются как на классических методах точного решения различных уравнений математической физики, так и на приближенных методах. К точным методам анализа можно- отнести [34]: метод разделения переменных, метод преобразования Лапласа, методы конечных интегральных преобразований и др. Однако в связи с тем, что уравнения СИ с распределенными параметрами, например [57], весьма разнообразны и сложны, а их анализ связан с решением краевых задач, довольно часто пользуются приближенными методами с заменой преобразователей с распределенными параметрами эквивалентными элементами с сосредоточенными параметрами. Весьма эффективны для анализа также моделирование на ЭВМ и использование метода конечных разностей, методов конечных и граничных элементов.
Даже из весьма краткой характеристики методов анализа математических моделей СИ можно сделать вывод о существовании довольно большого количества разнообразных методов и путей анализа. Поэтому рассмотрим некоторые из них, наиболее часто используемые на практике для исследования и определения основных характеристик СИ.
5.2. ТОЧНЫЕ МЕТОДЫ АНАЛИЗА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Дата добавления: 2015-11-18; просмотров: 769;