ПРИМЕР ДЛЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ.

Использование преобразований Лапласа рассмотрим па примере. Требуется определить импульсную характеристику СИ, описывае­мую уравнением

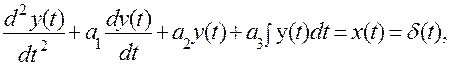(5.13)

где а_х, а₂, а₃ — постоянные коэффициенты, определяемые парамет­рами СИ.

Согласно правилам дифференцирования и интегрирования, а также теореме подобия и преобразованию единичной импульсной функции (табл. 5.1), уравнение в изображениях

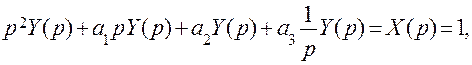
Поскольку это уравнение является алгебраическим, решение относи­тельно изображения выходной величины можно представить в виде

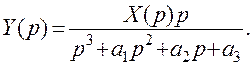
Для определения 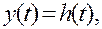необходимо найти обратное преобра­зование Лапласа полученного решения У (р), например, непосред­ственным интегрированием или, что значительно проще, разложив выражения У (р) на дроби, аналогичные приведенным для изобра­жений в табл. 5.1.

Используя правило разложения на простейшие дроби, предста­вим выражение для У (р) в виде суммы изображений, имеющих зна­менатели первой степени. Для этого необходимо найти корни по­линома знаменателя. Для случая вещественных корней р₁, р₂, р₃ выражение для У (р) можно записать в виде

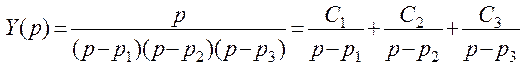(5.14)

где C₁, С₂, С₃ — произвольные постоянные.

Приведя правую часть этого уравнения к общему знаменателю и приравняв коэффициенты левой и правой частей при р с одинако­выми степенями, получим три уравнения с тремя неизвестными C₁, С₂, С_3:

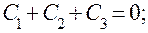
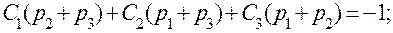
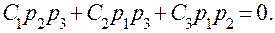
Определим неизвестные:

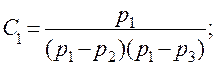
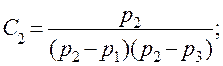
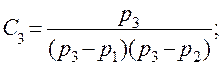
Воспользовавшись табл. 5.1 и уравнением (5.14), найдем обратное преобразование Лапласа У (р), то есть импульсную характеристи­ку СИ:

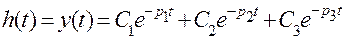(5.15)

Таким образом, для получения решения уравнений с использовани­ем преобразования Лапласа необходимо: найти изображения диф­ференциального уравнения с учетом начальных условий; получен­ное алгебраическое уравнение решить относительно изображения неизвестной функции; найти неизвестную временную функцию пу­тем обратного преобразования Лапласа (обычно путем разложения изображения на простейшие дроби).