Вероятностный подход к измерению информации.

Определить понятие “количество информации” довольно сложно. В решении этой проблемы существуют два основных подхода. В конце 40-х годов XX века один из основателей кибернетики, американский математик Клод Шенон, предложил вероятностный подход к измерению количества информации.

Сообщение, уменьшающее неопределенность знаний человека в два раза, несет для него 1 единицу информации. В качестве элементарной единицы измерения количества информации принят 1 бит.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Тогда количество информации, заключенное в этом сообщении , - х бит и число N связаны формулой Хартли

x=log₂N.

Например, сообщение о результате бросания монеты (количество равновероятных исходов равно 2) содержит х=1 бит информации (2^х = 2). Пусть в барабане для розыгрыша лотереи содержится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере ? Поскольку появление любого из 32 шаров равновероятно, то 2^х = 32 и х=5 бит. Рассмотрим еще один пример. При бросании игральной кости используют кубик с шестью гранями. Сколько бит информации получает каждый игрок при бросании кубика ? Так как выпадение каждой грани равновероятно, то 2^х = 6, откуда х=log₂6 » 2,585 бит.

Определим теперь, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.

Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.

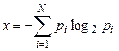
где p_i — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений

Легко заметить, что если вероятности p_i равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.

В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака “пробел” для разделения слов. По формуле Хартли x= log₂34 » 5,09 бит. Однако в словах различные буквы встречаются неодинаково часто. Вероятности частоты употребления различных букв вычисляются на основе анализа очень больших по объему текстов. Если это учесть, то по формуле Шеннона получим H=4,72. Вычисления показывают, что при равновероятных событиях мы получаем большее количество информации, чем при неравновероятных событиях.

При вычислении вероятности наступления какого-то события часто приходится вычислить количество различных исходов проведения опытов. При этом используют различные формулы комбинаторики – раздела дискретной математики, в котором решаются задачи выбора и расположения элементов некоторого множества в соответствии с некоторыми правилами.

Задача 1. На вершину горы ведет 7 дорог. Сколькими способами турист может подняться на гору и спуститься с нее если подъем и спуск осуществляется разными путями ?

Задача 2. В группе 30 человек. Необходимо выбрать старосту и профорга. Сколькими способами можно это сделать ?

Задача 3. Сколько существует трехзначных чисел с разными цифрами ?

Задача 4. Сколькими способами можно разместить на полке 4 книги ?

Правило произведения. Если из некоторого конечного множества
1-й объект можно выбрать k₁ способами,

2-й объект можно выбрать k₂ способами,

……………………………………………..

n-й объект можно выбрать k_n способами.

тогда произвольный набор, перечисленных n объектов, из данного множества можно выбрать k₁× k₂ … k_n способами.

Для нахождения числа различных перестановок из n элементов используют формулу P_n = n! Например, из цифр 3,5,7 можно составить 6 перестановок: 357, 375, 537, 573, 753, 735.

Задача 5. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1,2,3,4,5,6 при условии, что в числе цифры не повторяются ?

Задача 6. Сколькими способами могут расположиться в турнирной таблице 10 команд, если известно, что никакие две команды не набрали поровну очков ?

Пусть имеется некоторое множество, содержащее n элементов. Все элементы такого множества можно занумеровать, т.е. каждому элементу поставить в соответствие одно из натуральных чисел 1,2,…, n. Такие множества называются упорядоченными.

Любой упорядоченный набор из k элементов n-элементного множества называют размещением 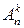из n элементов по k. Все эти подмножества отличаются друг от друга или составом элементов, или порядком их распределения. Но число элементов во всех этих подмножествах равно k.

Например, пусть Х={a,b,c}. Тогда по одному элементу можно образовать три размещения: (a), (b), (c); по два – шесть размещений: (a,b), (b,a), (a,c), (c,a), (b,c), (c,b). Для определения числа 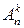размещений из n элементов по k используют формулу

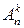= n(n-1)…(n – k +1) =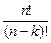

Задача 7. В турнире принимают участие 8 команд. Сколько различных предсказаний относительно распределения трех первых мест можно сделать ?

Задача 8. В семестре изучаются 14 предметов. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели должно быть 5 различных предметов ?

Задача 9. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, стал набирать их наудачу. Сколько вариантов ему надо перебрать, чтобы набрать нужный номер ?

Задача 10. Назовите все возможные комбинации из двух различных нот (всего нот семь: до, ре, ми, фа, соль, ля, си).
Иногда возникает необходимость не учитывать порядок элементов, входящих в размещение. Например, необходимо составить различные произведения из чисел 3,5,7. Таких произведений будет всего три: 3ž5, 3ž7, 5ž7, так как 3ž5=5ž3 и мы порядок не учитываем.

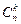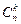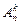Количество k-элементных подмножеств n-элементного множества называют сочетаниями и обозначают . Порядок элементов в подмножестве не имеет значения. Обратите внимание: отличие от : в сочетаниях не могут быть два одинаковых подмножества {a,b} и {b,a}.Два различных сочетания отличаются составом входящих в них элементов. Например, ниже выписаны всевозможные сочетания, составленные из 5 элементов 1,2,3,4 и 5 по 3 (столькими способами Вы можете выбрать 3 книги из 5): 123, 124, 125, 134, 135, 145, 234, 235, 245, 345

Число сочетаний из n элементов по k равно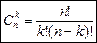

Задача 11. Сколько экзаменационных комиссий, состоящих из 7 членов, можно образовать из 14 преподавателей ?

Задача 12. В турнире принимали участие n шахматистов, и каждые 2 шахматиста встретились 1 раз. Сколько партий было сыграно ?

Задача 13. Поезд находится на одном из восьми путей. Сколько бит информации содержит сообщение о том, где находится поезд ?
Задача 14. Сколько бит информации получает игрок о масти при случайном вытаскивании карты из колоды ?

Задача 15. Тетрадь лежит на одной из двух полок - верхней или нижней. Сколько бит несет в себе сообщение, что она лежит на нижней полке?

Задача 16. Шарик находится в одной из 32 урн. Сколько единиц информации будет содержать сообщение о том, где он находится?

Задача 17. После реализации одного из равновозможных событий получили количество информации равное 10 бит. Какое количество возможных событий было первоначально ?

Задача 18. Какое количество информации получит первый игрок после первого хода второго игрока в игре "крестики - нолики" на поле 4 х 4 ?