Тема 3. Дифференцируемость и дифференциал
Аннотация.Дифференцирование это термин, обозначающий нахождение, как производных функций, так и их дифференциалов.
Ключевые слова: функция, производная, скорость, дифференциал.
Методические рекомендации по изучению темы:
После изучения лекционного материала и изучения презентационного материала с разбором решений необходимо выполнить задание №3.
Источники информации:
1. Берман Г.Н. Сборник задач по курсу математического анализа / Г.Н.Берман. — М.: Наука, 1977.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление / Я.С. Бугров, С.М. Никольский.— М.: Наука, 1988.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. — М.: Высшая школа, 2001.
4. Бесплатный ресурс для студентов – http://math24.ru/calculus-list.html
5. Образовательный математический сайт – http://www.exponenta.ru/
6. Учебные материалы - http://math.fizteh.ru/study/
7. Учебные пособия - http://kpfu.ru/main_page?p_sub=14502
Список сокращений:
Глоссарий:
Абсцисса - Одна из декартовых координат точки, обычно первая, обозначаемая буквой x.
Аргумент функции - Независимая переменная величина, по значениям которой определяют значения функции.
График - Кривая на плоскости, изображающая зависимость функции от аргумента.
Дифференцирование - Термин, обозначающий нахождение, как производных функций, так и их дифференциалов.
Касательная - Предельное положение секущей, проходящей через данную точку и другую точку кривой, неограниченно приближающуюся к данной.
Константа - Постоянная величина при рассмотрении математических и других процессов.
Вопросы для изучения:
3. Понятие дифференцируемости и дифференциала.
4. Связь дифференциала с производной.
Лекция 4.
Дифференциал
Пусть функция 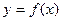 непрерывна в рассматриваемой точке х,
непрерывна в рассматриваемой точке х, 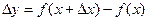 . Если
. Если 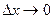 , то
, то 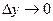 , т.е. обе эти величины – бесконечно малые при
, т.е. обе эти величины – бесконечно малые при 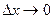 .
.
Считая 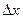 за основную бесконечно малую, выделим главную часть
за основную бесконечно малую, выделим главную часть 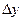 . Получим
. Получим 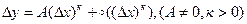 .
.
Допустим, что к = 1, т.е.
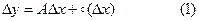 .
.
Если 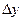 бесконечно малая высшего порядка чем
бесконечно малая высшего порядка чем 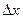 , т.е.
, т.е. 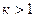 , то запись (1) можно сохранить, допуская А = 0.
, то запись (1) можно сохранить, допуская А = 0.
Так что 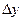 можно представить в виде (1), если
можно представить в виде (1), если 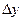 и
и 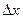 имеют один порядок (
имеют один порядок ( 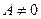 ) или
) или 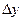 имеет высший порядок, чем
имеет высший порядок, чем 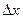 (А = 0).
(А = 0).
В первом случае говорят, что 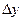 имеет главную линейную часть относительно
имеет главную линейную часть относительно 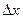 .
.
Определение 1. Функция 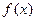 называется дифференцируемой в точке х, если приращение функции в этой точке
называется дифференцируемой в точке х, если приращение функции в этой точке 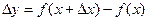 представимо в виде (1), где А – постоянная, не зависящая от
представимо в виде (1), где А – постоянная, не зависящая от 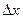 . Величина
. Величина 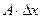 называется дифференциалом функции
называется дифференциалом функции 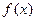 в точке х и обозначается
в точке х и обозначается 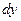 или
или 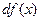 .
.
Таким образом 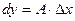 ,
, 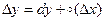 .
.
Теорема 1. Функция 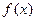 дифференцируема в точкех тогда и только тогда, когда она имеет в этой точке производную, причем
дифференцируема в точкех тогда и только тогда, когда она имеет в этой точке производную, причем
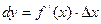 (1).
(1).
Доказательство. Необходимость. Пусть функция 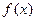 дифференцируема в точкех, т.е.
дифференцируема в точкех, т.е. 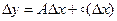 . Отсюда
. Отсюда 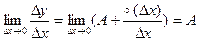 , т.е.
, т.е. 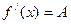 .
.
Достаточность. Пусть в точкех существует конечная производная 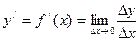 . Тогда
. Тогда 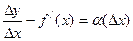 , где
, где 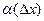 - бесконечно малая при
- бесконечно малая при 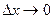 . Отсюда
. Отсюда 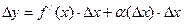 . Слагаемое
. Слагаемое 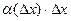 есть
есть 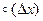 при
при 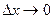 , т.к.
, т.к. 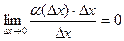 . Таким образом
. Таким образом 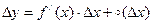 , где
, где 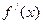 от
от 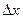 не зависит. Значит
не зависит. Значит 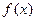 дифференцируема в точкех и
дифференцируема в точкех и 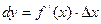 . Теорема доказана.
. Теорема доказана.
Полагая 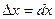 (дифференциал аргумента) из (1) получим
(дифференциал аргумента) из (1) получим
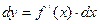 (2).
(2).
Из (2) имеем 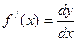 .
.
Пусть функции 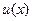 и
и 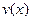 дифференцируемы в точкех. Тогда
дифференцируемы в точкех. Тогда
1) 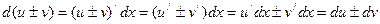 .
.
2) 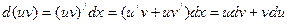 .
.
3) Пусть 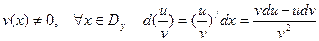 .
.
4) 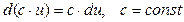 .
.
Лекция 5.
Дата добавления: 2015-11-18; просмотров: 793;
