Решите следующие задачи самостоятельно. Заданное графиком мгновенных значений (рис.1.9) синусоидальное напряжение представить в виде:

ЗАДАЧА 1.4

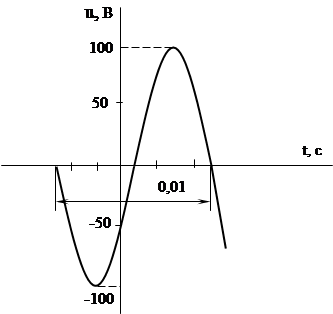Рис.1.9.

Заданное графиком мгновенных значений (рис.1.9) синусоидальное напряжение представить в виде:

1) тригонометрической функции;

2) комплексного числа;

3) показать комплекс на комплексной плоскости.

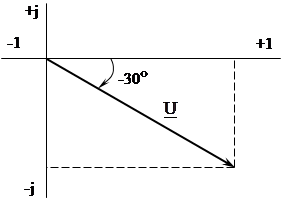Рис.1.10.

Ответ: 1. 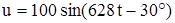В;

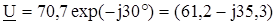2. В.

ЗАДАЧА 1.5

Комплекс 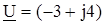А

1) изобразить на комплексной плоскости;

2) представить в виде тригонометрической функции;

3) представить в виде графика мгновенных значений, w = 3140 рад/с.

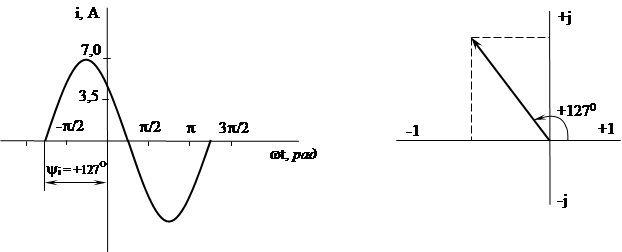Рис.1.11. Изображения функции i = 7,07sin(3140t + 127°) A.

Перейдем к рассмотрению второй целевой задачи.

Анализ электрических цепей переменного тока производится, как правило, комплексным методом.

Идея комплексного метода заключается в замене мгновенных значений синусоидально изменяющихся ЭДС, напряжений и токов, действующих в расчетной схеме, на изображающие их комплексные ЭДС, напряжения, токи:

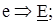
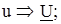
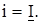
Параметры (сопротивление R, индуктивность L, емкость С) пассивных элементов схемы (резисторов, катушек индуктивности, конденсаторов) также заменяют их комплексными изображениями, которые учитывают сопротивления, оказываемые ими синусоидальному току, а также вносимый ими сдвиг по фазе между приложенным к этим элементам напряжениям и протекающим по ним токам:

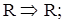
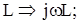
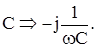
Интегродифференциальные уравнения, описывающие режимы в цепях синусоидального тока (u_R =Ri, u_L =L 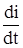, u_L = 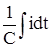) при изображении токов и напряжений в виде комплексов и введении комплексных сопротивлений превращаются в алгебраические, что значительно упрощает расчет цепей.

Закон Ома для участка цепи: .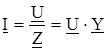

где Z – комплексное сопротивление участка;

Y – комплексная проводимость участка.

1-й закон Кирхгофа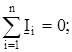

2-й закон Кирхгофа .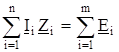

АЛГОРИТМ РЕШЕНИЯ

1. Заменить мгновенные значения ЭДС, напряжений и токов расчетной схемы на их комплексные изображения.

2. Заменить параметры пассивных элементов схемы на их комплексные изображения.

3. Рассчитать одним из методов расчета цепей комплексные значения искомых величин.

4. При необходимости перейти к мгновенным значениям искомых величин.

Рассмотрим применение комплексного метода анализа цепей синусоидального тока на примере определения напряжения на элементах цепи при их последовательном соединении.

ЗАДАЧА 1.6.

Дано:

i = 10sin(314t + 30°) A; R = 5 Ом; С = 318 мкФ; L = 47,8 мГн.

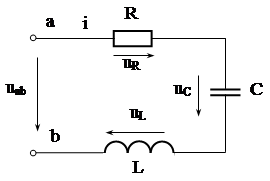Рис.1.12.

Определить комплексные напряжения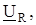

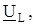
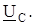
Записать мгновенные значения напряжений u_R(t), u_L(t), u_C(t).

Изобразить векторную диаграмму напряжений и тока.

РЕШЕНИЕ ЗАДАЧИ 1.6.

1. Согласно алгоритму, заменяем мгновенные значения напряжений и тока расчетной схемы на их комплексные изображения.

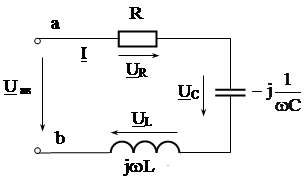Рис.1.13.

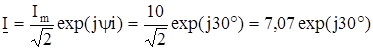A.

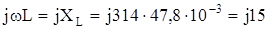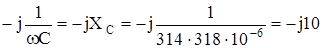2. Ом.

Ом.

3. По закону Ома для участка цепи:

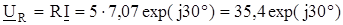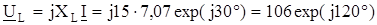В;

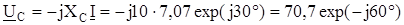В;

В;

Векторная диаграмма.

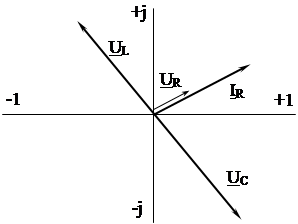Рис.1.14.

4. Мгновенные значения:

В;

В;

В.