Расчет зубьев на изгибную прочность
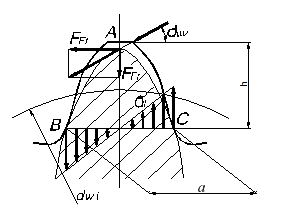
Рассмотрим зуб, нагруженный силой нормального давления 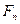
Перенесем силу 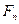 по линии ее действия в точку А и разложим на две составляющие – окружное усилие
по линии ее действия в точку А и разложим на две составляющие – окружное усилие  и радиальное усилие
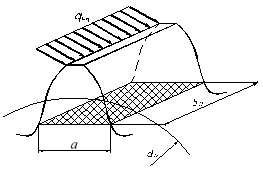
и радиальное усилие 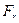 . Для определения опасного сечения в зуб впишем профиль балки равного сопротивления, который очерчивается квадратичной параболой с вершиной в точке А. В точках В и С, где ветви параболы касаются эвольвент бокового профиля зуба, нормальные напряжения изгиба имеют наибольшие значения.
. Для определения опасного сечения в зуб впишем профиль балки равного сопротивления, который очерчивается квадратичной параболой с вершиной в точке А. В точках В и С, где ветви параболы касаются эвольвент бокового профиля зуба, нормальные напряжения изгиба имеют наибольшие значения.
Напряжения от составляющей 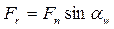 составляют 4 ─ 6 % от напряжения изгиба, поэтому ими можно пренебречь.
составляют 4 ─ 6 % от напряжения изгиба, поэтому ими можно пренебречь.
В соответствии с классической теорией плоского изгиба нормальные напряжения определяются по формуле
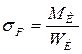 ,
,
где 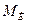 ─ изгибающий момент,
─ изгибающий момент,
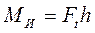 ,
,
Здесь примем Ft = 2 T/dw1.
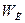 ─ момент сопротивления изгибу опасного сечения,
─ момент сопротивления изгибу опасного сечения,
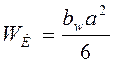 .
.
С учетом (1.28) и (1.29) запишем формулу для определения напряжений изгиба в виде
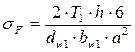 .
.
Обозначим
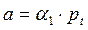 ;
;
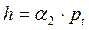 ,
,
где 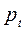 - окружной шаг,
- окружной шаг,
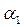 и
и 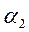 - численные коэффициенты. Введем в формулу коэффициент концентрации напряжений у основания зуба
- численные коэффициенты. Введем в формулу коэффициент концентрации напряжений у основания зуба 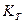 . Линейные величины имеют размерность миллиметры, крутящий момент T1 в Нм, поэтому T1 помножим на 103. С учетом того, что
. Линейные величины имеют размерность миллиметры, крутящий момент T1 в Нм, поэтому T1 помножим на 103. С учетом того, что 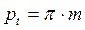 , преобразуем формулу (1.31)
, преобразуем формулу (1.31)
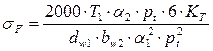 . (1.32)
. (1.32)
Обозначим через 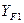 коэффициент формы зуба шестерни:
коэффициент формы зуба шестерни:
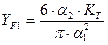
Введем в формулу коэффициент нагрузки 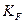 , аналогичный коэффициенту
, аналогичный коэффициенту 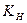 , который учитывает реальные условия работы передачи
, который учитывает реальные условия работы передачи
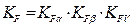 , (1.33)
, (1.33)
где 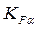 ─ коэффициент, учитывающий распределение нагрузки между зубьями;
─ коэффициент, учитывающий распределение нагрузки между зубьями; 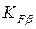 ─ коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца;
─ коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца;
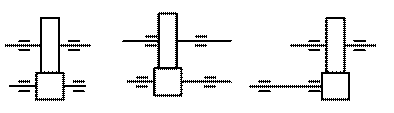
KFV ─ коэффициент, учитывающий динамическую нагрузку в зацеплении.
С учетом принятых обозначений из (1.32) получаем формулу для проверочного расчета зубьев шестерни цилиндрической передачи на прочность по напряжениям изгиба
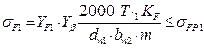 . (1.34)
. (1.34)
В формуле (1.34)  ─ допускаемое напряжение изгиба зуба шестерни;
─ допускаемое напряжение изгиба зуба шестерни; 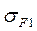 ─ расчетное напряжение зуба шестерни;
─ расчетное напряжение зуба шестерни; 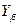 ─ коэффициент, учитывающий наклон зубьев.
─ коэффициент, учитывающий наклон зубьев.

Для прямозубой передачи 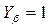 , для косозубой
, для косозубой 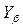 рассчитывается по зависимости
рассчитывается по зависимости 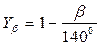 . (1.35)
. (1.35)
Формула проверочного расчета зубчатого колеса на изгибную прочность запишется в виде
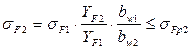 . (1.36)
. (1.36)
Учитывая, что 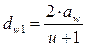 , из (1.34) получим формулу для предварительного расчета модуля из условия изгибной прочности:
, из (1.34) получим формулу для предварительного расчета модуля из условия изгибной прочности:
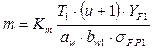 , (1.37)
, (1.37)
где 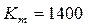 для прямозубой передачи.
для прямозубой передачи.
В предварительном расчете коэффициент формы зуба принимается 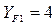 для прямозубых колес.
для прямозубых колес.
Дата добавления: 2015-11-18; просмотров: 1305;
