По контактным напряжениям

В основу расчета зубьев на прочность по контактным напряжениям положена теория статически сжатых цилиндров, разработанная Герцем.

Величину этих контактных напряжений определяют по формуле

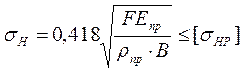, (1.19)

где 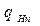─ равномерно распределенная нагрузка, ;

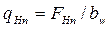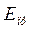─ приведенный модуль упругости, который зависит от модулей упругости Е₁ и Е₂ материалов сжимаемых цилиндров;

;

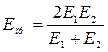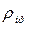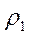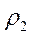─ приведенный радиус кривизны, определяемый радиусами и сопряженных цилиндров,

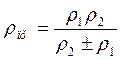(знак «+» ─ для внешнего касания цилиндров, знак «─» ─ для внутреннего касания);

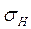─ расчетное контактное напряжение; 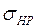─ допускаемое контактное напряжение.

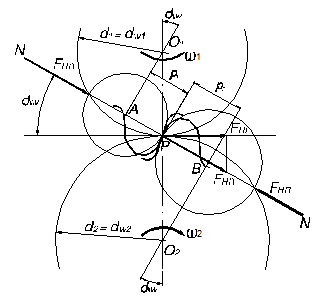
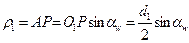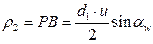.(1.) . (2)

В формулах (1) и (2) 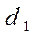и 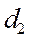─ делительные диаметры зубчатых колес;

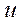─ передаточное число зубчатой передачи.

Приведенный радиус кривизны

.

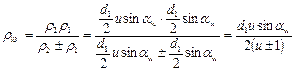Приведенный модуль упругости с учетом того, что сопряженные колеса изготовлены из стали, т.е. Е₁=Е₂

.

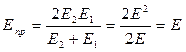Выразим равномерно распределенную нагрузку 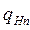, действующую на зубья через крутящий момент на ведущем звене (шестерне):

,

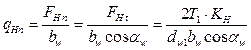где 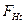─ окружное усилие; Т₁ – крутящий момент на шестерне; 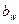─ ширина зубчатого венца (длина зуба).

K_Н – коэффициент нагрузки, увеличивающий крутящий момент Т₁ с учетом реальных условия работы передачи

Подставим значения 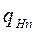, 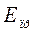и 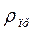в формулу Герца

.

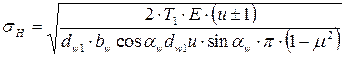Введем следующие обозначения:

Z_м – коэффициент, учитывающий механические свойства материалов шестерни и колеса,

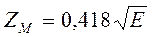
Z_Н – коэффициент, учитывающий форму сопряженных поверхностей зубьев,

.

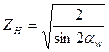Для некорригированных колес, а также колес с высотной коррекцией, в основном используемых в зубчатых передачах, угол зацепления .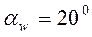

В связи с тем что в процессе работы передачи в зацеплении может находиться не одна пара зубьев, происходит изменение длины контактных линий, учитываемое коэффициентом Z_ε :

,

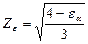где 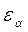─ коэффициент перекрытия.

С учетом введенных коэффициентов формула (1.22) примет вид

.

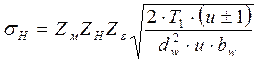Выразим b_w = ψ_ba ∙a_w , а диаметр 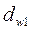через межосевое расстояние : .

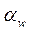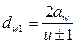Введем в формулу (1.23) коэффициент нагрузки К_н , увеличивающий крутящий момент Т₁ с учетом реальных условия работы передачи:

,

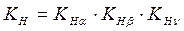где 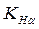─ коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубой передачи ;

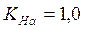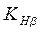─ коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого колеса. Коэффициент K_Hβ зависит от поверхностной твердости зубьев, ширины зубчатого венца и схемы передачи;

K_HV ─ коэффициент динамической нагрузки, зависит от степени точности зубчатых колес, которая назначается в зависимости от окружной скорости.

После подстановки и преобразований получим следующие выражения расчетов прямозубых зубчатых передач, изготовленных из черных металлов:

.

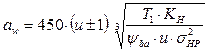Во всех формулах в сочетании 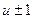знак «+» соответствует внешнему зацеплению колес, а знак «─» ─ внутреннему.

Коэффициент нагрузки К_H , увеличивающий крутящий момент Т₁ с учетом реальных условия работы передачи:

,

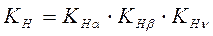где 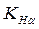─ коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубой передачи ;

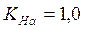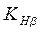─ коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого колеса.

Коэффициент K_Hβ зависит от поверхностной твердости зубьев, ширины зубчатого венца и схемы передачи;

K_HV ─ коэффициент динамической нагрузки, зависит от степени точности зубчатых колес, которая назначается в зависимости от окружной скорости.