Методы и средства измерения углов и конусов.

Для контроля углов применяют различные средства: угольники, угловые меры, конические калибры, угломеры, механические и оптические делительные головки, гониометры, синусные линейки и др. Угольники, калибры и угловые меры являются жесткими контрольными инструментами, они имеют определенные значения углов. Угольники подразделяются на цельные (рис. 28, а) и составные (рис. 28, б). Угловые меры – плитки (рис. 28, в) выпускаются наборами с таким расчетом, чтобы из трех – пяти мер можно было составлять блоки в пределах от 10 до 90⁰; их изготовляют в виде плиток толщиной 5 мм с точностью угла 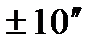(1-й класс) и 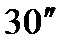(2-й класс). Они имеют или один рабочий угол или четыре рабочих угла: .

Угловые меры в основном применяют для поверки и градуировки различных средств измерения углов, но они могут применяться и непосредственно для измерения углов у деталей машин.

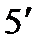Для измерения углов у деталей чаще всего пользуются универсальными угломерами: нониусными с величиной отсчета , оптическими с величиной отсчета , индикаторными с величиной отсчета .

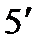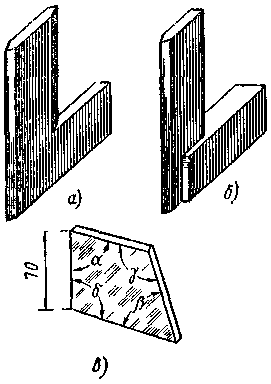
Рис. 28. Виды жестких измерительтельных средств:

а – цельный угольник, б – составной, в – угловая мера.

Угломер с нониусом (рис. 29) состоит из трех основных частей: жестко скрепленных линейки 1 и лимба 2, который имеет полукруглую форму; жестко скрепленных линейки 5 с сектором 3 и дополнительного угольника 6, которым пользуются при измерении острых

углов (менее 90⁰). Линейка 5 вращается на оси 4, связанной с лимбом. На дуге лимба 2 нанесена шкала с ценой деления 1⁰, а на дуге сектора 3 – нониус, который дает возможность отсчитывать дробные части шкалы.

Рис. 29. Нониусный угломер.

Для измерения острых углов (менее 90⁰) к линейке 5 присоединяют дополнительный угольник 6.

Нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы лимба 2, - число минут.

При измерении тупых углов (более 90⁰) дополнительный угольник 6 не нужен, но в этом случае к показаниям, снятым по шкале, необходимо еще прибавлять 90⁰.

Находят применение также оптические угломеры, имеющие две линейки и корпус, в котором размещен стеклянный диск со шкалой, разделенной на градусы и минуты.

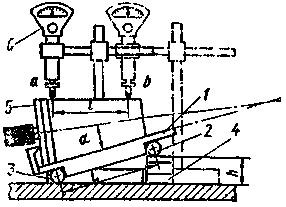
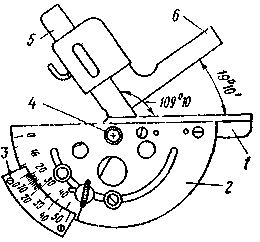
Рис. 30. Схема измерения угла конуса на синусной линейке.

Отчет производится после того, как положение угломера зафиксировано зажимным рычагом.

Косвенные методы контроля конусов. Наиболее точными и широко применяемыми являются косвенные методы измерений, при которых измерят не непосредственно углы конусов, а линейные размеры, геометрически связанные с углами.

После определения значения этих линейных размеров расчетом находят и значения углов.

Измерение с помощью линейки. Синусные линейки, выпускаемые инструментальной промышленностью, делятся на три типа: тип I – без опорной плиты, тип II – с опорной плитой, тип III – с двумя опорными плитами и двойным наклоном.

Предметный столик 1 (рис. 30) синусной линейки имеет два ролика 2 и 3 с определенным расстоянием между ними L. Если под одним из роликов подложить блок 4 из плоскопараллельных концевых мер размером h, то предметный столик наклонится на угол и его можно определить по формуле:

.

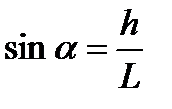При измерении угла конуса проверяемое изделие устанавливают на предметный столик, ориентируя его так, чтобы измеряемый угол находился в плоскости, перпендикулярной роликам синусной линейки (для этого используют боковые поверхности предметного столика). Установив изделие 5 на предметный столик 1, под ролик подкалывают блок из плоскопараллельных концевых мер 4. Размер блока определяют по формуле

,

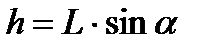где - номинальное значение измеряемого угла.

При разности показаний измерительной головки 6 в двух положениях на измеряемой длине можно определить отклонения измеряемого угла ( ) от номинального значения по формуле

.

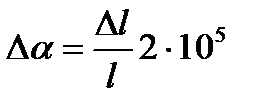Действительную величину угла можно определить, подобрав такой блок плиток, при котором показания измерительной головки не будет отличаться на всей измеряемой длине.

Измерение наружных конусов с помощью роликов. Этот косвенный метод измерения (рис. 31) угла конуса изделия 1 осуществляется при использовании плиты 2, двух роликов 3 одинакового размера (можно использовать ролики от роликовых подшипников), концевых мер 4 и микрометра с ценой деления 0,01 мм или рычажного с ценой деления 0,002 мм.

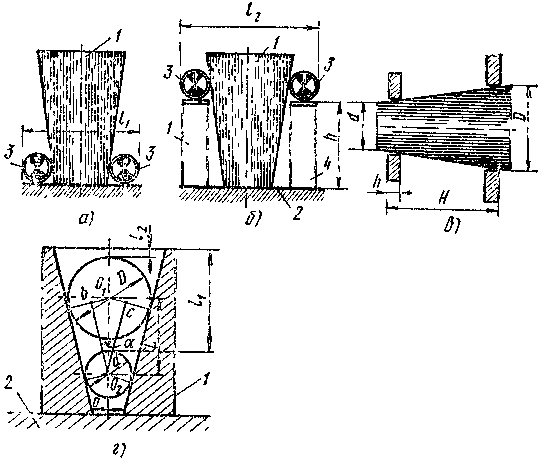
Рис. 31. Схемы измерения угла конуса с помощью калиброванных

роликов (а, б),колец (в), шариков (г).

Сначала измеряют размер по диаметрам роликов 3 (рис. 31,а), затем под ролики подкладывают блоки из концевых мер 4 одинакового размера 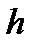и определяют размер 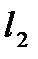(рис. 31,б). Зная размеры 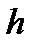, , 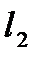находят конусность по формуле

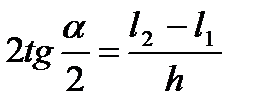или ,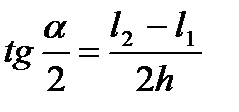

По такому же принципу измеряют конусность у вала с помощью двух калиброванных колец (рис. 31,в) с заранее известными диаметрами D и d и толщиной 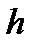. После надевания колец на конус вала измеряют размер H и определяют тангенс угла по формуле

.

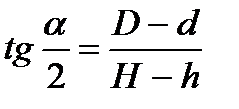Измерение внутренних конусов. Угол внутреннего конуса определяют с помощью двух шариков, диаметры которых заранее известны, и глубиномера (рис. 31,г).

Втулку 1 ставят на плиту 2, закладывают внутрь шарик малого диаметра d и измеряют при помощи глубиномера (микрометрического или индикаторного) размер , затем закладывают шарик большего диаметра D и измеряют размер 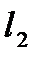. При таком методе измерения конусность втулки определяют по формуле:

.

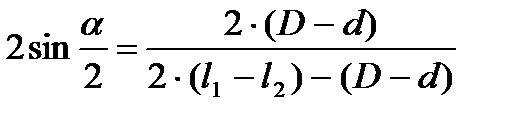Контроль конусов калибрами

Контроль калибрами (рис. 32) основан на проверке отклонений базорасстояния по методу осевого перемещения калибра относительно проверяемой детали или на проверке по краске.

Рис. 32. Конусные калибры:

а – втулка, б – пробка, в – скоба.

Калибрами для проверки наружных конусов служат втулки (рис. 32, а) или скоба (рис. 32, в), а для внутренних конусов – пробки (рис. 32, б), со стороны большого диаметра которых наносятся риски на расстоянии от торца калибра, равном допуску базорасстояния .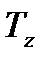

Торец проверяемых конических вала и втулки при сопряжении с калибром не должен выходить за пределы рисок или уступа на калибре. Если это условие нарушено, то угол конуса выходит из установленных пределов (допуска).

Конусные калибры – втулки проверяют по контрольным калибрам – пробкам. Контрольные калибры изготовляют с повышенной точностью конусности и проверяют универсальными средствами.

Вопросы для повторения:

1. Сколько степеней точности установлено для допусков на угловые размеры и почему допуск на угол уменьшается с увеличением длины меньшей стороны угла?

2. Назовите примеры применения конических соединений и их преимущества в сравнении с цилиндрическими соединениями.

3. Начертите конус и покажите основные параметры его.

4. Что называется базорасстоянием и в какой зависимости находится изменение его величины от допусков на диаметры конуса и конусности?

5. Как устроен угломер с нониусом и какие углы им можно измерять?

6. Расскажите о косвенных методах измерения угла наружного и внутреннего конусов.

7. Как осуществляется контроль наружных и внутренних конусов коническими калибрами?

Литература: [1, глава VI, стр. 151…168]

Лекция 7. ДОПУСКИ, ПОСАДКИ И СРЕДСТВА ИЗМЕРЕНИЯ

РЕЗЬБОВЫХ СОЕДИНЕНИЙ

Основные элементы метрической крепежной резьбы

и допуски на них

В машиностроении применяют различные резьбовые соединения: цилиндрические, конические, трапецеидальные и др. Эти резьбы имеют ряд общих признаков, а так как наиболее распространенными являются цилиндрические крепежные резьбовые соединения с треугольным профилем, то применительно к ним и будут рассмотрены допуски, методы и средства контроля.

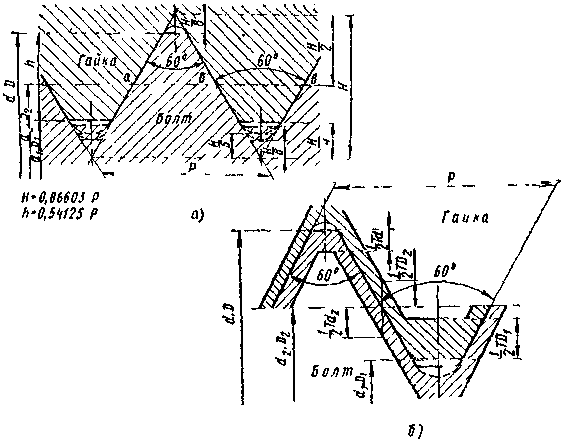
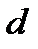Профиль метрической цилиндрической резьбы (рис. 33, а) представляет собой равносторонний треугольник с углом при вершине , равным 60⁰. Основными параметрами резьбы, общими для наружной резьбы (болта) и внутренней резьбы (гайки), являются: наружный диаметр и 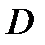, внутренний диаметр 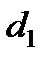и 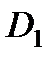, средний диаметр 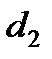и 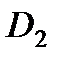, шаг резьбы 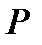, угол профиля , угол между стороной витка и перпендикуляром к оси резьбы 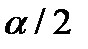, теоретическая высота витка , рабочая высота витка резьбы 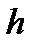. При измерении угла профиля и расчетах допусков учитывается угол 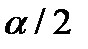, так как при нарезании резьбы ее профиль может быть завален на сторону так, что с правой стороны 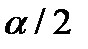будет больше или меньше, чем 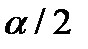с левой стороны, а в целом весь угол профиля может быть равен 60⁰.

Рис. 33. Метрическая цилиндрическая резьба:

а – профиль резьбы, б – схема расположения полей допусков.

Под средним диаметром понимают диаметр воображаемого, соосного с резьбой, цилиндра, который делит профиль резьбы так, что толщина витка, ограниченная на рис. 33, а буквами а – б, равна ширине впадины, ограниченной буквами б – в. Шаг резьбы – это расстояние вдоль оси резьбы между параллельными сторонами двух рядом лежащих витков.

Единой системой допусков и посадок СЭВ для метрической резьбы с размерами от 0,25 до 600 мм предусмотрены три стандарта: СТ СЭВ 180-75 определяет профиль резьбы; СТ СЭВ 181-75 – диаметры и шаги; СТ СЭВ 182-75 – основные размеры. Предельные отклонения и допуски резьбовых соединений с зазорами устанавливает СТ СЭВ 640-77.

Значения диаметров резьбы разбиты на 3 ряда (1, 2 и 3-й). При выборе диаметров резьбы предпочтительным является первый ряд. Второй ряд диаметров резьбы берется, если диаметры 1-го ряда не удовлетворяют требованиям конструктора; в последнюю очередь диаметры берутся из 3-го ряда. По числовой величине шага резьбы для диаметров 1-64 мм делятся на две группы: с крупным шагом и мелкие, а резьбы диаметром свыше 64 мм, (до 600 мм) имеют только мелкие шаги.

Допуски для цилиндрической крепежной резьбы ( ) установлены на следующие параметры: на средний диаметр болта и гайки в виде величин 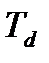и , (поле допуска для гайки расположено в плюс, а для болта – в минус от номинального размера); на наружный диаметр болта 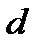и на внутренний диаметр гайки .

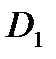Допуски на наружный диаметр гайки и внутренний диаметр болта не установлены. Технология нарезания резьбы и размеры резьбообразующих инструментов (метчиков, плашек и др.) гарантируют, что наружный диаметр резьбы гайки не будет меньше теоретического, а внутренний диаметр резьбы болта – больше теоретического.

На шаг резьбы и угол профиля в отдельности допуски не установлены, а возможные отклонения по ним допускаются за счет изменения среднего диаметра резьбы в пределах его допуска. Такая компенсация погрешностей шага и угла за счет допуска 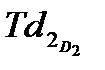, возможна потому, что шаг и угол геометрически связаны со средним диаметром.