Уравнение емкости - резервуар неизменной вместимости.

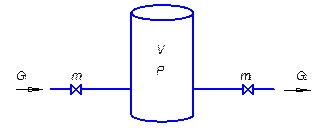
Рис. 3.3. Схема резервуара для газа.

V-емкость резервуара, заполненного газом, G₁- количество притекающего газа, G₂- количество вытекающего газа, m₁, m₂- координаты, определяющие положение распределительных органов- задвижек резервуара на входе и выходе газа, Р- давление газа в резервуаре.

1. В установившемся режиме

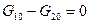. (3-29)

2. При нарушении равенства расходов путем воздействия на распределительные органы согласно закону сохранения материи

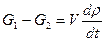, (3-30)

где ,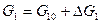

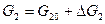
Предположим, что в неравновесных процессах состояние газа в резервуаре изменяется политропно: 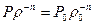, n-показатель политропы.

Продифференцировав уравнение политропы, получим

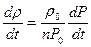и подставим в уравнение (3-30)

Для малых отклонений независимых переменных уравнение (3-30) станет 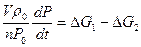(3-31)

где 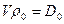-массовый вес газа.

Предположим: , ,

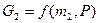тогда для малых колебаний имеем

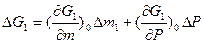
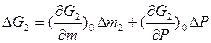
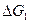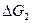Подставив выражения для и в уравнение (3-31) и представив переменные в относительных величинах, получим уравнение газового объема

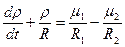, (3-32)

где ; ;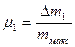

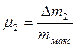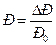
или в операторной форме 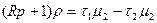(3-33)

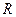-динамическая постоянная для емкост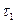и, и 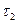- коэффициенты

; .

; ; .

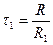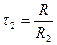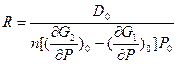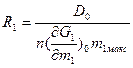Частные производные для постоянных коэффициентов уравнения (3-33) и находят по статическим характеристикам ОР, как ОР давления газа (Рис.3.4) и характеристика для регулировочных задвижек. (Рис. 3.5)

Рис. 3.4. Статические характеристики резервуара газа.

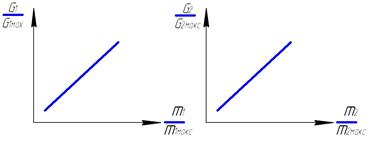
Рис. 3.5. Статические характеристики регулировочных органов.

Элементы, из которых составлена система регулирования могут существенно различаться по физической природе протекающих процессов, но сами процессы при этом будут описываться одинаковыми дифференциальными уравнениями. Сходство дифференциальных уравнений означает, что рассматриваемые объекты (элементы) математически подобны и что они обладают одинаковыми или близкими динамическими свойствами.