Дифференциальные уравнения

теплопроводности и конвективного

теплообмена

18.1 Дифференциальное уравнение теплопроводности

В соответствии с первым законом термодинамики теплота, передаваемая твёрдому телу из окружающей среды, при отсутствии работы деформации полностью трансформируется во внутреннюю энергию тела.

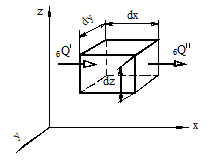Уравнение теплового баланса для элемента с величиной рёбер (рисунок 18.1) в однородном твёрдом теле имеет вид:

, (18.1)

где - элементарная теплота, передаваемая через грани выделенного элемента в направлении осей x,y,z ; dU - изменение внутренней энергии элемента.

В направлении оси x через грань dydz за время dt поступает в соответствии с законом Фурье теплота

За то же время через противоположную грань, расположенную на расстоянии dx от первой и имеющую температуру , из элемента передается теплота

Результирующая теплота, подведенная теплопроводностью к элементу в направлении оси х, равна

(18.2)

Аналогично определяется результирующая теплота в направлении осей y и z :

(18.3)

Изменение внутренней энергии элемента составляет

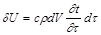(18.4)

C учетом (18.2-18.4) уравнение (18.1) имеет вид:

(18.5)

После сокращений в уравнении (18.5) получается:

(18.6)

Выражение (18.6) называют дифференциальным уравнением теплопроводности. Его записывают и в таком виде:

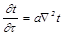, (18.7)

где - коэффициент температуропроводности, характеризующий темп изменения температуры;

- оператор Лапласа.

Уравнение (18.7) описывает в самом общем виде процесс теплопроводности и устанавливает связь между временными и пространственными изменениями температуры тела. Для его решения применительно к определенной задаче необходимо математическое описание конкретных условий, называемых условиями однозначности, которые включают:

временные или начальные условия, определяющие распределение температуры в теле в начальный момент;

геометрические условия, характеризующие форму и размеры тела;

физические условия, задаваемые теплофизическими параметрами вещества, составляющего рабочее тело;

граничные условия, определяющие характер взаимодействия тела с окружающей средой на границе соприкосновения.

Начальные условия имеют смысл при нестационарной теплопроводности и обычно задаются законом распределения температур по всему объему тела для момента времени t = 0.

Граничные условия могут быть заданы несколькими способами.

Если для любого момента времени известно распределение температур на границе тела, то это называют граничными условиями первого рода.

При граничных условиях второго рода задаётся поверхностная плотность теплового потока (а, следовательно, и температурный градиент) в каждой точке поверхности тела для любого момента времени. Температура на поверхности тела при этом неизвестна.

Граничные условия третьего рода предполагают, что известна температура окружающей среды и закономерность взаимосвязи между этой температурой и температурой тела. В условиях конвективного теплообмена связующим является уравнение Ньютона-Рихмана.

Решение дифференциального уравнения теплопроводности совместно с условиями однозначности позволяет получить температурное поле исследуемого тела для любого частного случая в любой момент времени. Такое аналитическое решение позволяет в ряде случаев избавиться от проведения сложных и дорогостоящих экспериментальных работ.