Существует не более пяти различных видов правильных многогранников.
Докажем, что грани правильных многогранников не могут быть правильными n-угольниками, где n³6.
Пусть гранями правильного многогранника служат правильные шестиугольники. Градусная мера каждого их внутреннего угла равна 120°. В каждой вершине правильного многогранника сходится не менее трех граней, тогда сумма градусных мер плоских углов при вершине многогранника не менее 3×120°=360°, а это невозможно, так как по теореме 2 сумма градусных мер всех плоских углов выпуклого многогранного угла меньше 360º. Градусная мера каждого внутреннего угла правильного многоугольника с большим числом сторон больше 120°, поэтому они не могут оказаться гранями правильного многогранника.‡
Таким образом, гранями правильного многогранника могут быть лишь треугольники, четырехугольники и пятиугольники. Рассмотрим возможные случаи:
| № | Число граней, сходящихся в каждой вершине | Вид многоугольников, которые служат гранями многогранника | Сумма плоских углов при вершине | Название правильного многогранника |
| треугольник | 60°×3=180° < 360° | Тетраэдр  Развёртка: Развёртка: 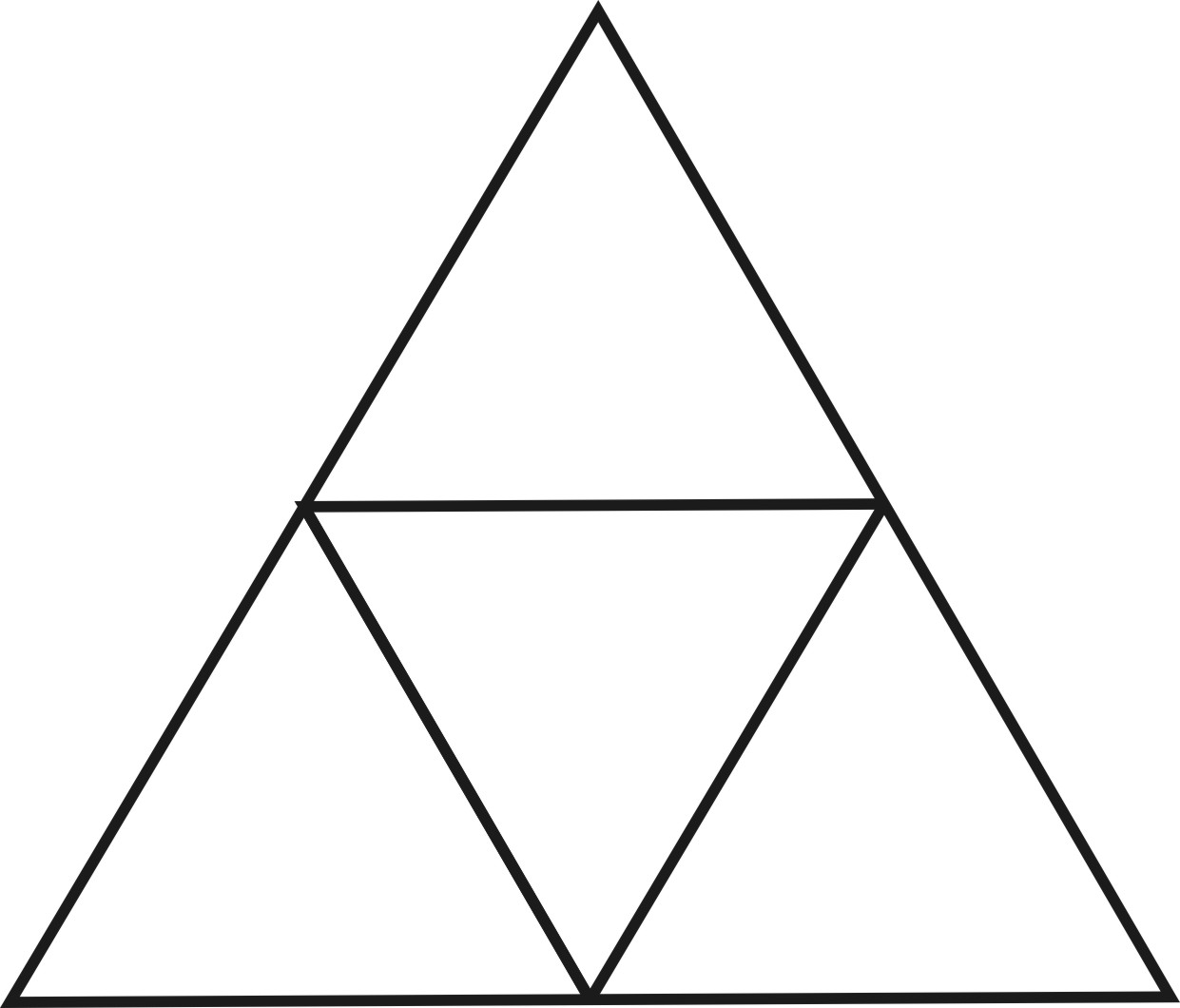 4 грани
4 грани
| ||
| четырёхугольник | 90°×3=270° <360° | Гексаэдр (куб) 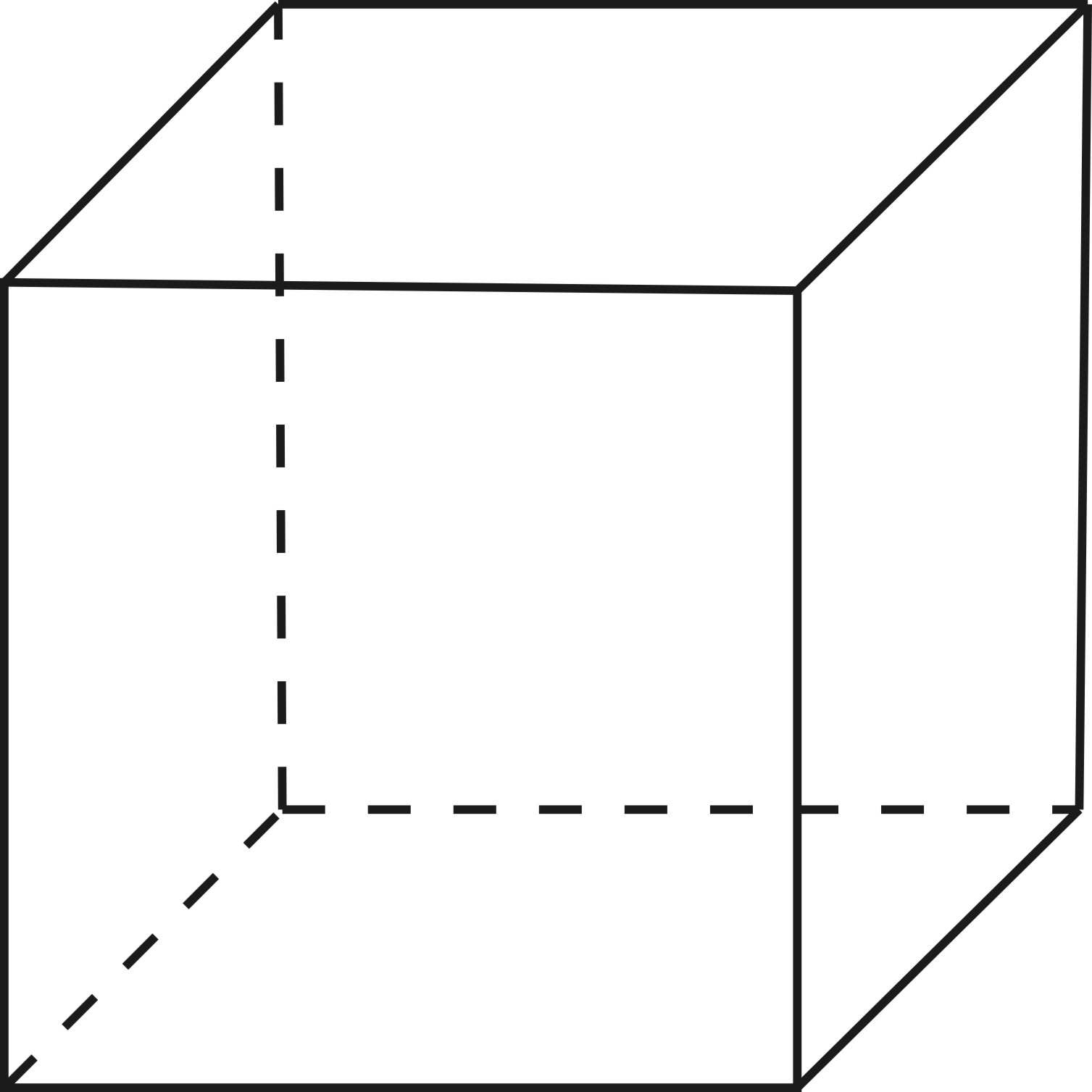 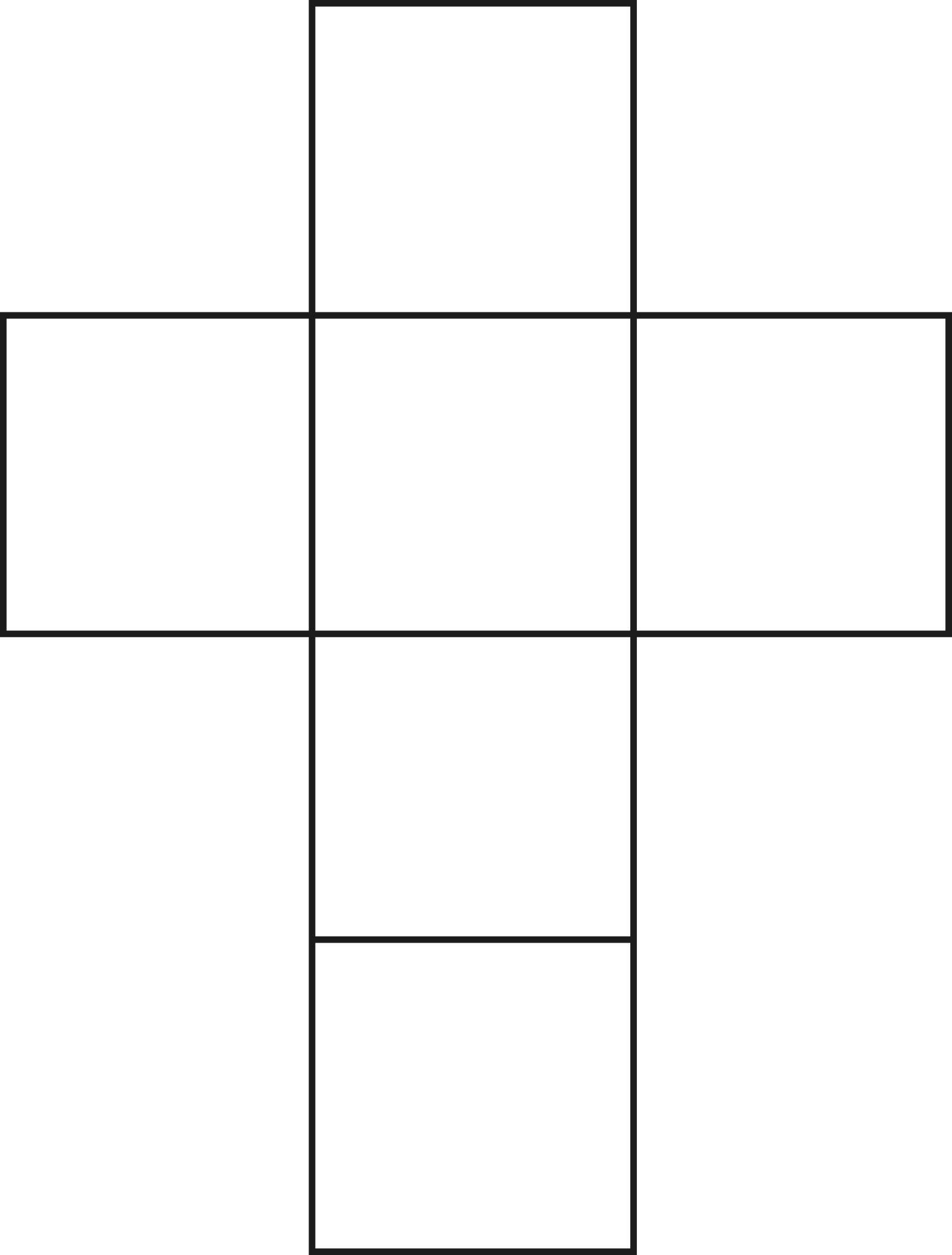 6 граней
6 граней
| ||
| пятиугольник | 108°×3=324° <360° | Додекаэдр 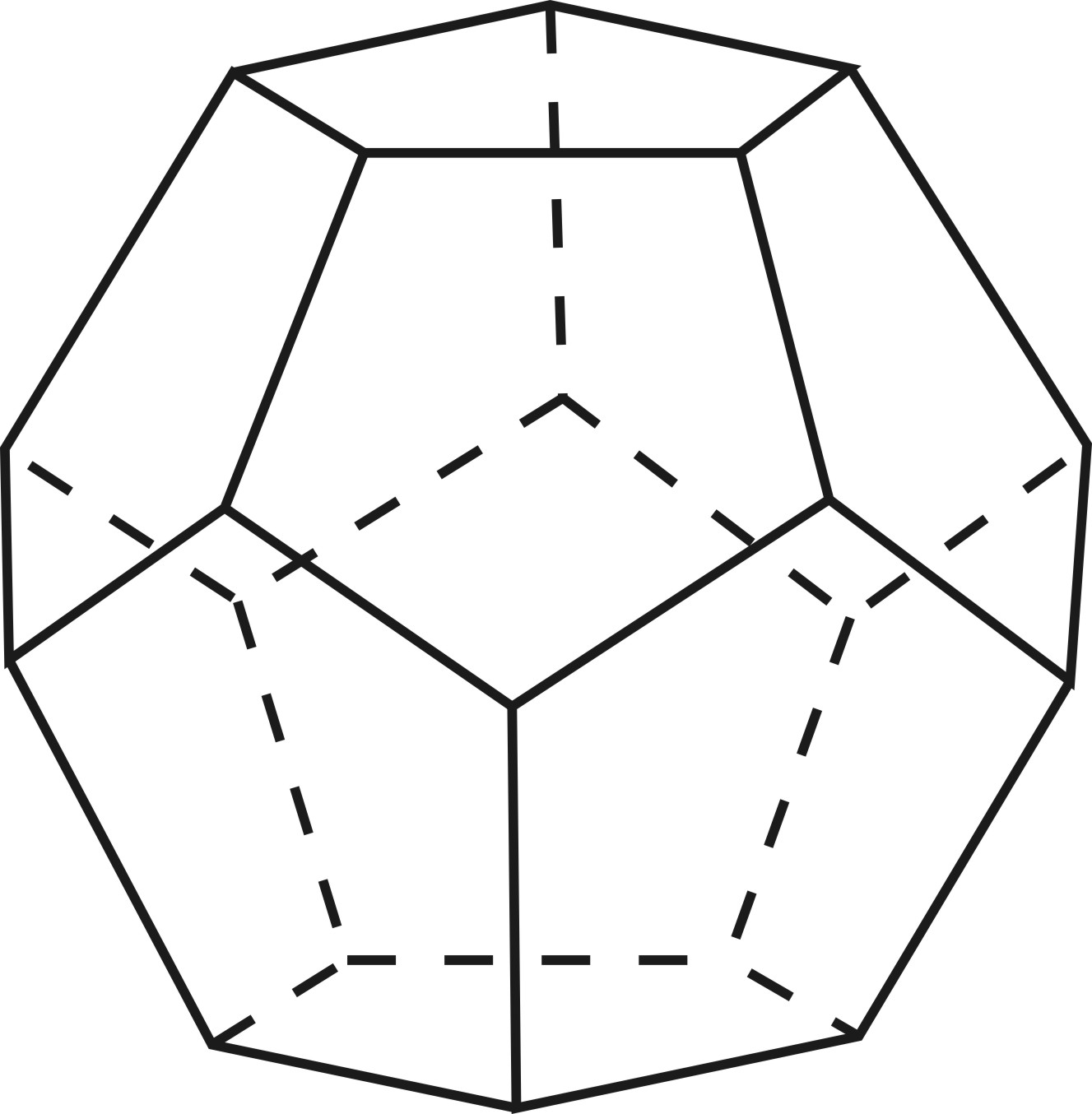 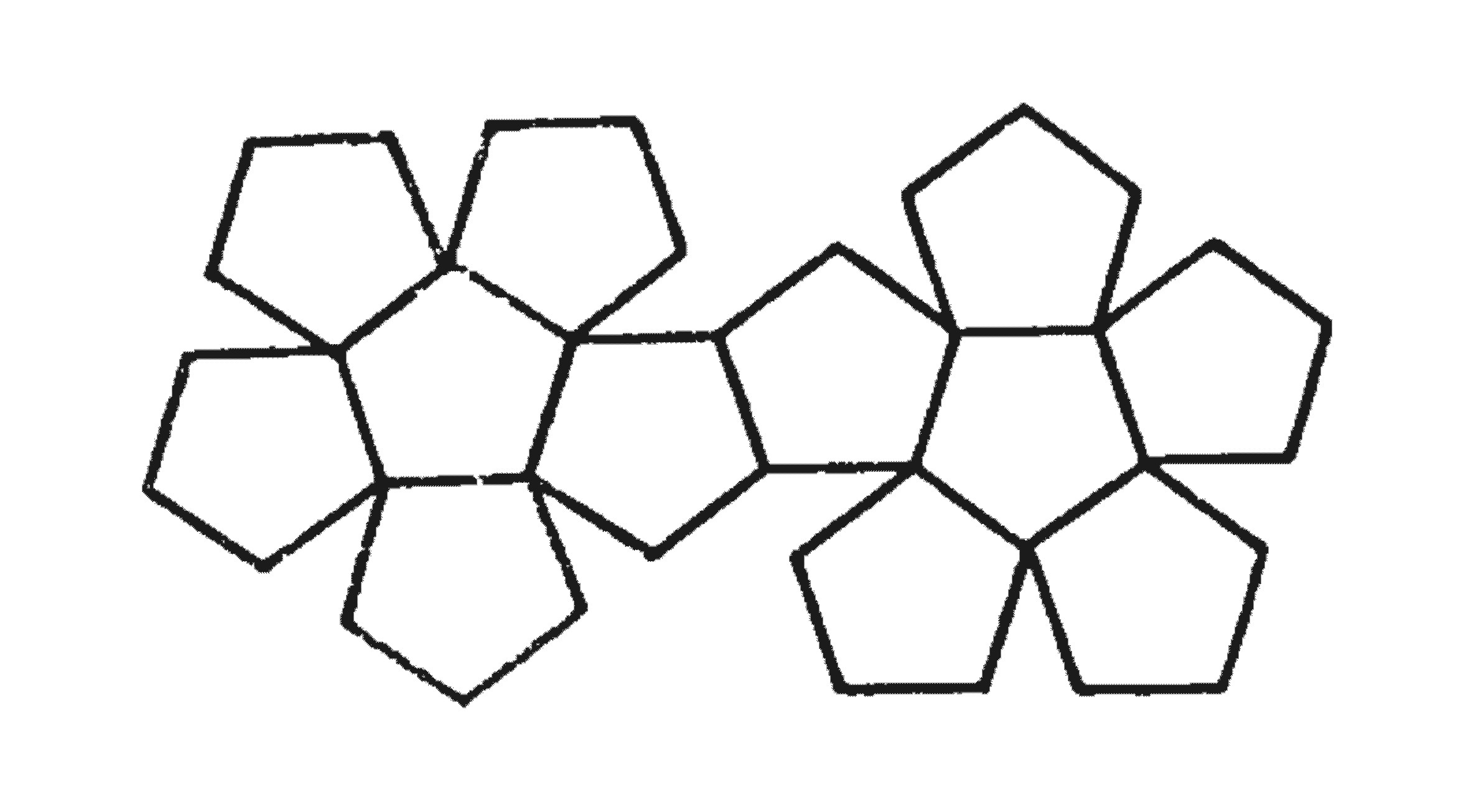 12 граней
12 граней
| ||
| треугольник | 60°×4=240° < 360° | Октаэдр 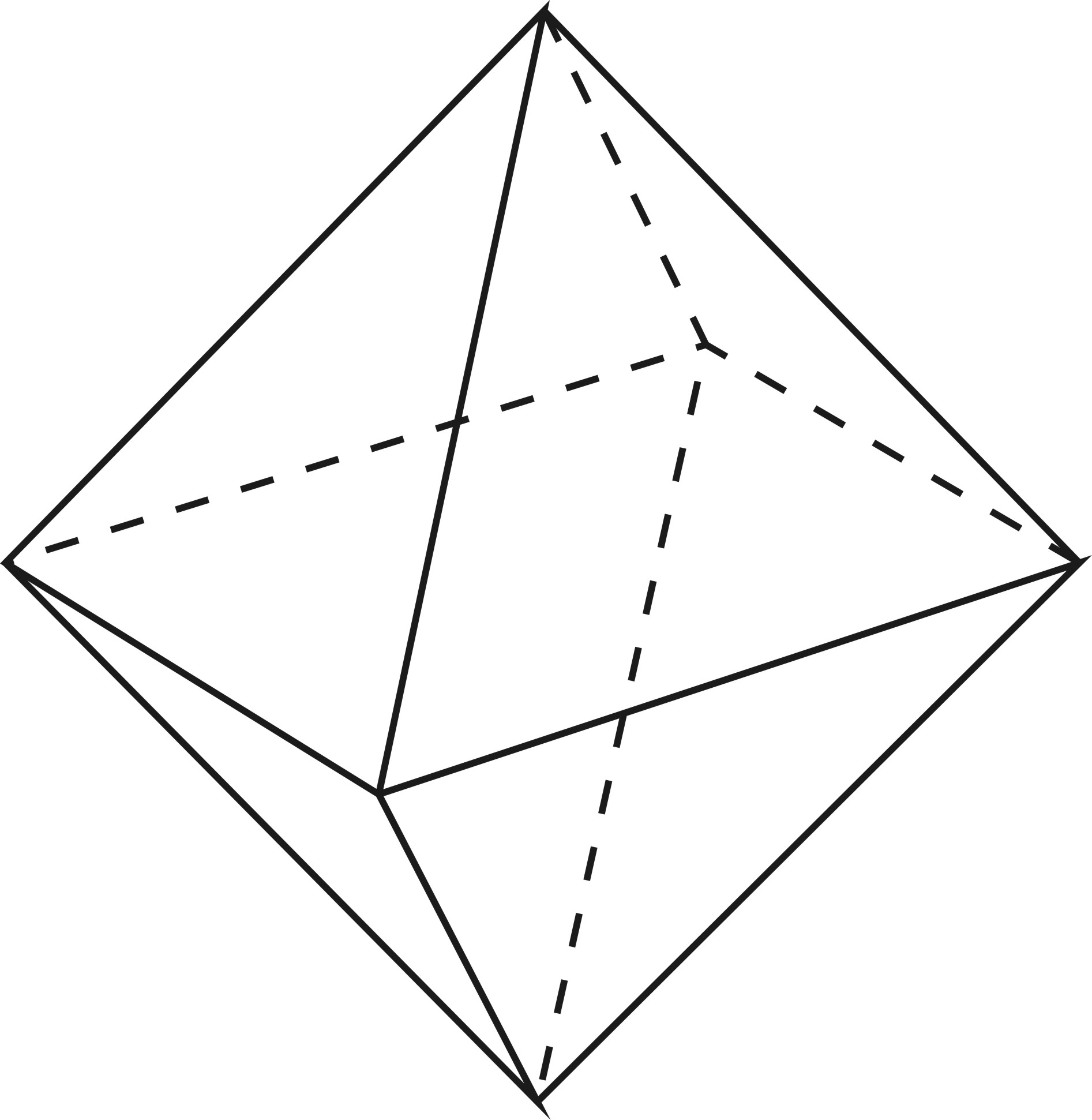  8 граней
8 граней
| ||
| | | 90°×4 = 360° !!!!! | ||
| | | 108°×4 > 360° !!!! | ||
| треугольник | 60°×5=300° < 360° | Икосаэдр 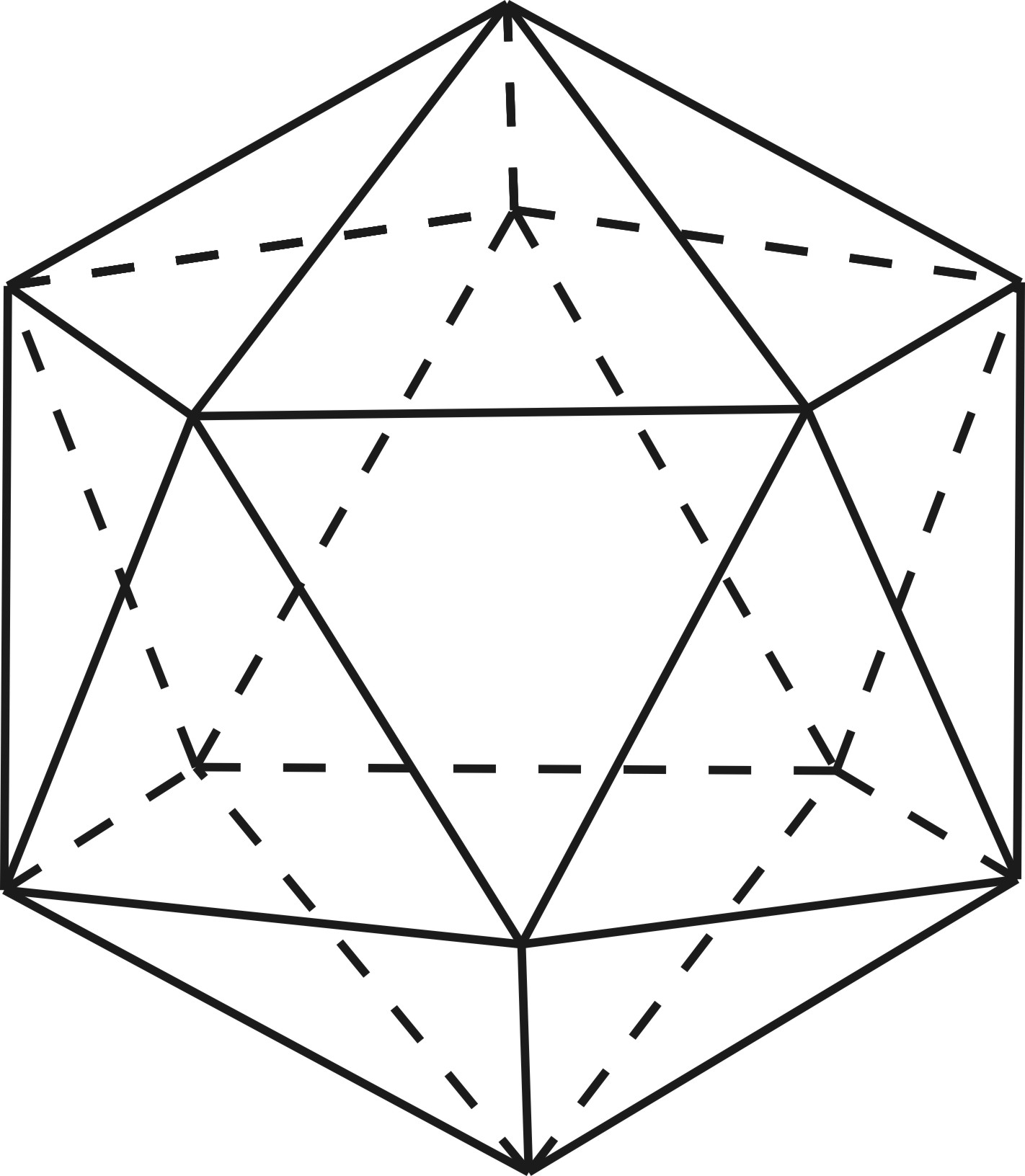 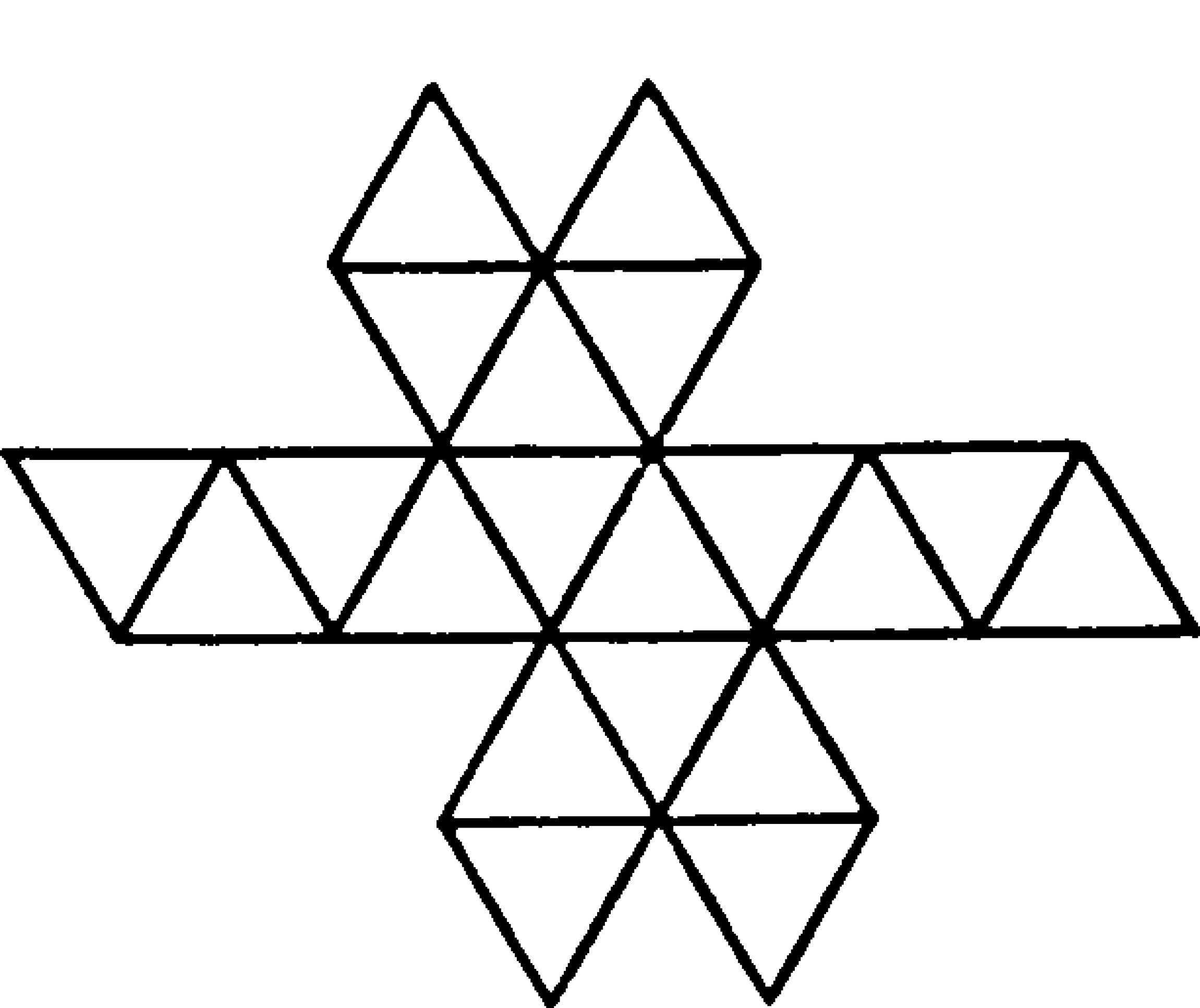 20 граней
20 граней
|
Проверьте самостоятельно справедливость теоремы Эйлера для всех видов правильных многогранников.
| Вид многогранника | b | g | r |
| Тетраэдр | |||
| Гексаэдр (куб) | |||
| Октаэдр | |||
| Додекаэдр | |||
| Икосаэдр |
Дата добавления: 2015-11-10; просмотров: 9468;
