Этапы процесса подобного моделирования

1. Выбирается из числа существующих или создается специальный объект - модель с математическим описанием

F(y_м, x_мi, t_мj, P_Mi) =0,

сходственным с описанием оригинала.

2. Определяются критерии подобия для оригинала и модели p_о и p_м.

3. Составляются в общем виде масштабные уравнения на основе выражений для критериев подобия

p_о / p_м = 1

4. Вводятся масштабы сходственных переменных y_o и y_м, x_oi и x_мi, t_oj и t_мj и масштабным уравнениям придается окончательный вид.

Масштабы можно принять равными

m_y = y_O / y_M; m_xi = x_Oi / x_Mi; m_tj = t_Oj / t_Mj

5. Анализируется система масштабных уравнений. Зависимые уравнения из системы исключаются. Установление противоречивости системы масштабных уравнений означает невозможность подобия.

6. Выбираются конкретные численные значения масштабов с учетом реальных предельных значений сходственных переменных.

7. Устанавливаются условия однозначности модели, подобные условиям однозначности оригинала.

8. Рассчитываются функциональные зависимости x_Мi = x_Мi(t_Мj, x_Оi = x_Оi(t_Оj).

Пример: требуется подвергнуть моделированию некоторый материальный объект, описываемый уравнением

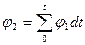, (2.71)

где j₁ и j₂ - угловые величины, измеряемые в радианах; t - время в секундах.

1. В качестве объекта - модели выбирается математический аналог (генератор линейно изменяющегося напряжения), описываемый сходственным уравнением

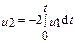, (2.72)

где u1, u2 - напряжения постоянного тока, измеряемые в вольтах; t - время в секундах.

Полагаем в (2.71) t = t_O, а в (2.72) t = t_М и вводим операторы дифференцирования D_O = d /dt_O, D_M = d / dt_M. Тогда уравнения (2.71) и (2.72) примут вид дифференциальных уравнений первого порядка

D_Oj₂ = j₁, D_Mu₂ = -2u₁

с нулевыми начальными условиями. Множитель при j₁ в первом уравнении, равный единице, имеет размерность 1/с (!).

2. Приведя дифференциальные уравнения к безразмерной форме

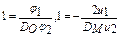
определяем критерии подобия

.

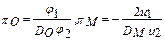3. Составляется в общем виде масштабное уравнение

.

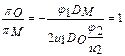Отсюда следует, что в одной из двух пар сходственных переменных j₁ и u₁ или j₂ и u₂ переменные должны иметь разные знаки.

4. Вводим масштабы

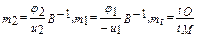
и получаем масштабное уравнение в окончательном виде

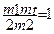
5. Полученное единственное масштабное уравнение, конечно, непротиворечиво.

6. Согласно полученному масштабному уравнению можно принять m₁ = 2B^{-1, m₂} = 10B^-1. Тогда m_t = 10. При таком масштабе времени процессы, происходящие в модели, аналогичны по форме процессам в оригинале, но протекают в 10 раз быстрее.

7. Нулевые начальные условия являются подобными условиями однозначности при любых масштабах.

8. Для расчета функции u₁ = u₂(t_M), подобной заданной функции j₁ = j₂(t_O), имеем

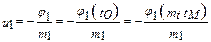
или окончательно

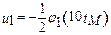
В данном случае материальная подобная модель, согласно вышеприведенной терминологии, является формальной.

Классификация видов подобия и моделирования

Схема классификации (рис.10) основывается на взаимосвязи понятий моделирования и подобия, в соответствии с которой модель и оригинал находятся между собой в отношении подобия (подобны друг другу).

Классификация указывает, какие виды подобия и соответствующего им моделирования могут быть использованы при решении практических задач.

Первоначально виды подобия и моделирования разделяются по признаку полноты учёта и воспроизведения на модели параметров оригинала и процессов в нём. То есть разделяются на полное и неполное подобие, и на соответствующие им виды моделирования (полное и неполное). Как полное, так и неполное виды подобия могут быть приближёнными.

Далее виды моделирования разделяются на мысленное (I. Теоретическое, II. Аналитическое) и материальное в зависимости от способа их материальной реализации.

I. Мысленное теоретическое моделирование – это моделирование на основе мысленных представлений, т.е. построение модели происходит в сознании человека.

II. Мысленное аналитическое – это моделирование использующее аппаратуру для подтверждения мысленных представлений.

Материальное моделирование – это реально-практический вид моделирования. Как мысленное, так и материальное виды моделирования могут быть либо детерминированными, т.е. предполагающие отсутствие случайных воздействий (возмущений); либо стохастическими, т.е. отображающие вероятностные события; либо обобщёнными, т.е. отображающие оригинал (явления происходящие в нём) условно.

В свою очередь мысленное моделирование подразделяется на наглядное, знаковое и математическое мысленное.

Наглядное моделирование – создание наглядных моделей, отображающие явления и процессы, протекающие в объекте.

К этому виду моделирования относятся:

гипотезы (это мысленные представления) в форме воображаемых моделей. Например, модели атомов. Гипотетическое моделирование используется, для построения формальных моделей.

Рис. 3. Классификация видов подобия и моделирования.

2. Наглядные аналоги. Например, модель атома созданная мысленно, но реализована материально.

Рис.15 Классификация видов подобия и моделирования

Макеты. Например, уменьшенная копия здания, т.е. макет – это модель, дающая геометрическое подобие.

Знаковое моделирование – создание модели, основные свойства которой выражаются с помощью системы знаков или символов, т.е. вводятся условные обозначения отдельных понятий знаками. Например, формула химического соединения.

Знаковое моделирование разделяется:

· Моделирование на основе условно-знаковых представлений. Например, если состояние или соотношение химических элементов во время реакции описать в виде условных знаков, то получим модель химической реакции, которая будет представлена условно;

· Моделирование на основе топологических представлений;

· Моделирование на основе графовых представлений.

Математическое мысленное моделирование – это моделирование на основе схем замещения, алгоритмов и программ, а также структурных схем. Этот вид моделирования устанавливает связь между логическим и чувственным, т.е. подкрепляет абстрактное мышление привычными образами, которые помогают исследователю воспринять и анализировать явления.

Схемы замещения. Например, схемы замещения трансформаторов и электродвигателей, которые отображают математические уравнения и их физическую интерпретацию с помощью более простых и наглядных объектов. Возьмём, к примеру, схему замещения преобразователь - двигатель постоянного тока:

где e_д – противо-ЭДС двигателя.

Структурные схемы – это схемы, отражающие функциональные связи между подсистемами сложных систем. Например, структурная схема ДПТ:

Рис. 17 Структурная схема преобразователь – ДПТ.

Алгоритмы и программы – моделирование условными знаками процессов описанных дифференциальными уравнениями. Например, система дифференциальных уравнений описывающих преобразователь – ДПТ:

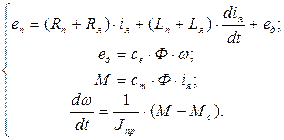(4)

Натурное моделирование – это моделирование предполагающее проведение исследований на реальном объекте. По виду подразделяются на:

· производственный эксперимент – эксперимент, проводимый во время производственного процесса на действующем предприятии, может рассматриваться как модель, отвечающая задачам производства, его развития и совершенствования;

· обработку и обобщение натурных данных, т.е. сведений о явлениях или процессах, происходящих в натуре, с целью построения соответствующих моделей;

· моделирование путём обобщения производственного опыта, в отличии от моделирования на основе производственного эксперимента (который специально организуют) пользуются имеющимся материалом. Например, в отделах главных энергетиков любого предприятия скапливаются данные о потреблении предприятием электрической энергии. Накопление этих данных специально не планировалось, но на их основе можно построить модель динамики потребления электроэнергии предприятием.

Физическое моделирование – это вид моделирования, при котором исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием.

1. временное моделирование – если исследуются процессы протекающие во времени;

2. пространственный вид моделирования – если моделирование предназначено для изучения процессов, действие которых не рассматривается во времени, а только в пространстве;

3. временное - пространственное – объединяет в себе понятия временного и пространственного видов моделирования.

Математическое материальное. Это вид моделирования, при котором физика процессов не сохраняется. Основа его состоит в способности математических уравнений описывать объекты, процессы и т.д.