Метод интегральных соотношений
Метод интегральных соотношений, предложенный Г. И. Баренблаттом, по аналогии с методами пограничного слоя в потоке вязкой жидкости позволяет получить приближенные решения некоторых задач нестационарной фильтрации упругой жидкости с нужной точностью. Метод основан на следующих предпосылках.
1. В каждый момент времени пласт делится на конечную возмущенную область и невозмущенную область, где движение отсутствует.
2. В возмущенной области распределение давления представляется в виде многочлена по степеням координаты х или r (в случае радиального потока добавляется еще логарифмический член) с коэффициентами, зависящими от времени, так что:
для прямолинейно-параллельного потока
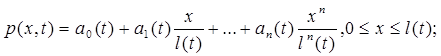(5.99)
для плоскорадиальной фильтрации
(5.100)
где число членов n выбирается в зависимости от желаемой точности решения.
3. Коэффициенты многочлена а0, а1, а2, ..., аn, а также размер области возмущения l(t) (или R(t)) находятся из условий на галерее (или на забое скважины), из условий непрерывности давления и гладкости кривой давления на границе области возмущения, а также из особых интегральных соотношений, которые получаются следующим образом.
В случае притока к галерее правая и левая части уравнения пьезопроводности (5.21) умножаются на хk (где k=0, 1, 2, ...) и интегрируются по всей возмущенной области:
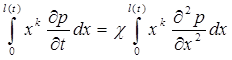. (5.101)
Для случая притока к скважине берется дифференциальное уравнение (5.49), его правая и левая части умножаются на rk (где k = 1, 2, ...) и проводится интегрирование по всей возмущенной области:
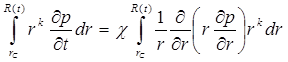. (5.102)
Если в уравнения (5.101) и (5.102) подставить соответственно выражения (5.99) и (5.100) и проинтегрировать, то получатся недостающие соотношения для определения коэффициентов а0(t), а1(t),... и l(t) или R(t).
Первое из этих интегральных соотношений (при k = 0, если рассматривается приток к галерее, и при k = 1 для притока к скважине) представляет собой уравнение материального баланса и из него находится координата границы возмущенной области l(t) или R(t).
Если принять в формуле (5.99) n = 1, а в формуле (5.100) n = 0, то получатся решения, соответствующие методу ПССС (5.81), (5.82), (5.89)-в зависимости от условий на галерее или на забое скважины; если же n = 2 в (5,99), то из метода интегральных соотношений вытекает, как частный случай, метод А. М. Пирвердяна.
В качестве примера решим методом интегральных соотношений задачу о плоскорадиальной неустановившейся фильтрации упругой жидкости к скважине радиусом rc пущенной в эксплуатацию в момент t = 0 с постоянным дебитом Q. В начальный момент давление во всем пласте постоянно и равно рк.
Распределение давления в возмущенной области пласта rc≤ r ≤ R(t) зададим в виде
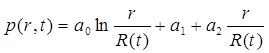, (5.103)
т. е. возьмем многочлен первой степени.
Коэффициенты а0, а1,и а2 определяются из условий на забое скважины и на границе возмущенной области.
Условие на забое согласно (5.50) имеет вид:
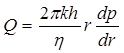, при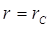 
. (5.104)
На границе возмущенной области имеем:
р=рк при r = R(f),
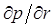= 0, при г = R(t),
где второе условие представляет собой условие гладкости кривой. Определенные из этих условий коэффициенты имеют вид:
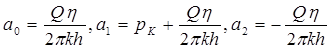(5.106)
(слагаемые, пропорциональные rc или r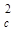 
, отброшены вследствие их малости).
Подставив выражения (5.106) в правую часть формулы (5.103), получим:
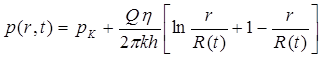. (5.107)
Закон движения границы возмущенной области R(t) находится из уравнения материального баланса (5.76) с учетом (5.86) (это уравнение можно получить из интегрального соотношения (5.102) при k = 1).
Значение средневзвешенного пластового давления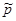 
в возмущенной области определяется при использовании распределения давления (5.103):
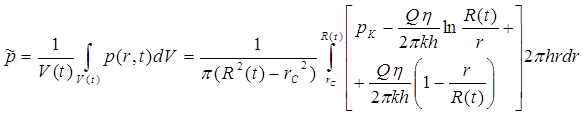
Проведя интегрирование и пренебрегая в полученном выражении членами, содержащими r 
(вследствие их малости), получим:
,
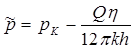а тогда согласно (5.86)
. (5.108)
Подставив выражения (5.86) для V(t) и (5.108) в уравнение материального баланса (5.76), после несложных преобразований найдем:
,
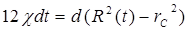откуда после интегрирования получим:
.
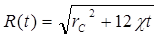Следовательно, распределение давления (5.103) в возмущенной области будет иметь вид
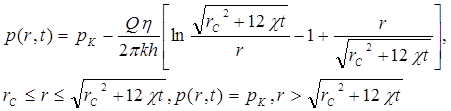(5.109)
Относительная погрешность δ при расчетах депрессии pк—рс(t) по формуле (5.109) для различных значений параметра Фурье fo=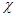 
t/r , составляет: δ = - 4,9% при fo = 100; δ =- 4% при fo = 103; δ = - 3,2% при fo = 104.
Таким образом, приближенное значение депрессии ∆рс по методу интегральных соотношений занижено по сравнению с точным.
Метод «усреднения»
Суть метода «усреднения», предложенного для решения задач фильтрации Ю. Д. Соколовым и Г. И. Гусейновым заключается в том, что в дифференциальном уравнении упругого режима (5.49) производная от давления по времени ∂р/∂t усредняется по всей возмущенной области и заменяется некоторой функцией времени
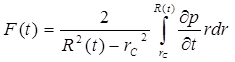, (5.110)
значение которой определяется из начальных и граничных условий.
Тогда уравнение (5.49) принимает вид
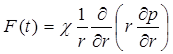. (5.111)
Эта замена упрощает дифференциальное уравнение и облегчает его интегрирование.
Будем определять распределение давления при неустановившемся притоке упругой жидкости к скважине при постоянном дебите Q. При этом условия на забое и на границе возмущенной области имеют вид (5.104) и (5.105). Интегрируя уравнение (5.111) по r и учитывая условия (5.104) и (5.105), можно получить:
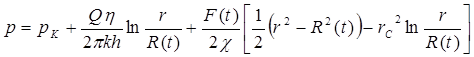(5.112)
Из второго условия (5.105) определяется функция F(t) в виде
. (5.113)
Подставляя выражение (5.113) в (5.112) и пренебрегая членами с r ,
найдем:
. (5.114)
Для определения координаты возмущенной области R(t) надо продифференцировать по t равенство (5.114), результат подставить в (5.110) и учесть выражение (5.113) для F(t). Тогда получим:
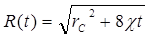. (5.115)
Сопоставление формулы (5.114) с учетом (5.115) с точным решением (5.62) показывает, что относительная погрешность определения депрессии
pк - рс не превосходит 5%,
В заключение отметим приближенный результат, полученный Э. Б. Чекалюком. Для скважины, пущенной в эксплуатацию с постоянным забойным давлением, он предлагает определять дебит по формуле Дюпюи (5,85), в которой радиус возмущенной области
.
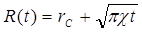Эта формула очень важна для практики, поскольку простого точного решения задачи об отборе упругой жидкости при условии рс = const не существует. Расчетами показано, что формула Э. Б. Чекалюка очень точна, относительная погрешность при определении дебита не превышает 1%.
Дата добавления: 2015-11-10; просмотров: 1852;