Математические модели объектов проектирования на микроуровне
Математические модели деталей и процессов на микроуровне отражают физические процессы, протекающие в сплошных средах и непрерывном времени. Независимыми переменными в этих моделях являются пространственные координаты и время. В качестве зависимых переменных выступают фазовые переменные, такие как потенциалы, напряженности полей, концентрации частиц, деформации и т. п. Взаимосвязи переменных выражаются с помощью уравнений математической физики — интегральных, интегро-дифференциальных или дифференциальных уравнений в частных производных. Эти уравнения составляют основу ММ на микроуровне.
Для получения законченной математической модели, используемой в задачах проектирования, необходимо дополнительно выполнить ряд процедур:
· выбрать краевые условия. Краевые условия представляют собой сведения о значениях фазовых переменных и (или) их производных на границах рассматриваемых пространственных и временных областей;
· дискретизировать задачу. Дискретизация подразумевает разделение рассматриваемых пространственных и временных областей на конечное число элементарных участков с представлением фазовых переменных конечным числом значений в избранных узловых точках, принадлежащих элементарным участкам;
· алгебраизировать задачу — аппроксимировать дифференциальные и интегральные уравнения алгебраическими.
Используют два основных подхода к дискретизации и алгебраизации краевых задач, составляющие сущность методов конечных разностей (МКР) и конечных элементов (МКЭ). С помощью любого из этих методов формируется окончательная модель, исследуемая при выполнении различных процедур анализа проектируемого объекта.
Пользователь САПР средствами входного языка задает исходную информацию о конфигурации проектируемого объекта, о способе дискретизации — разделения среды на элементы, — о физических свойствах участков среды. Формирование модели объекта, т. е. разделение среды на элементы, выбор математических моделей элементов из заранее составленных библиотек, объединение моделей элементов в общую систему уравнений, так же как и решение получающихся уравнений, осуществляется автоматически на ЭВМ.
Основные уравнения математической физики, используемые в моделях проектируемых объектов. Процессы, протекающие в техническом объекте при его функционировании, по своей физической природе могут быть разделены на:
· электрические;
· тепловые;
· магнитные;
· оптические;
· механические;
· гидравлические и т. п.
Каждому типу процессов в математической модели соответствует своя подсистема, основанная на определенных уравнениях математической физики. Рассмотрим примеры уравнений, составляющих основу математических моделей технических объектов на микроуровне.
Электрические процессы в современных полупроводниковых приборах с достаточной точностью удается описать с помощью уравнений непрерывности и Пуассона. Уравнения непрерывности выражают скорости изменения концентраций свободных носителей заряда и записываются отдельно для дырок и электронов:
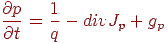
| (15.6) | ||
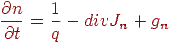
| (15.7) | ||
где p и n — концентрации дырок и электронов, соответственно; q — заряд электрона; gP и gn — скорости процесса генерации-рекомбинации, соответственно, дырок и электронов;
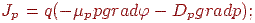
| (15.8) | ||
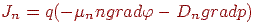
| (15.9) | ||
где q — плотности дырочного и электронного токов; μp, μn — подвижности; Dp, Dn — коэффициенты диффузии дырок и электронов; 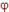 — электрический потенциал.
— электрический потенциал.
Уравнения (15.8)-(15.9) показывают, что причинами изменения концентрации носителей могут быть неодинаковость числа носителей, втекающих (и вытекающих) в элементарный объем полупроводника (тогда div J  0), и нарушение равновесия между процессами генерации и рекомбинации носителей. Уравнения (15.8) и (15.9), называемые уравнениями плотности тока, характеризуют причины протекания электрического тока в полупроводнике: электрический дрейф под воздействием электрического поля (grad
0), и нарушение равновесия между процессами генерации и рекомбинации носителей. Уравнения (15.8) и (15.9), называемые уравнениями плотности тока, характеризуют причины протекания электрического тока в полупроводнике: электрический дрейф под воздействием электрического поля (grad 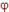
 0) и диффузию носителей при наличии градиента концентрации. Уравнение Пуассона характеризует зависимость изменений в пространстве напряженности электрического поля Е = –grad
0) и диффузию носителей при наличии градиента концентрации. Уравнение Пуассона характеризует зависимость изменений в пространстве напряженности электрического поля Е = –grad 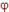 от распределения плотности электрических зарядов ρ:
от распределения плотности электрических зарядов ρ:
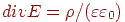
| (15.10) |
где ε — относительная диэлектрическая проницаемость среды; ε0 — диэлектрическая постоянная.
В качестве краевых условий в моделях полупроводниковых приборов используют зависимости потенциалов на контактах от времени, принимают значения концентраций носителей на границе между внешним выводом и полупроводником равными равновесным концентрациям ро и n0, для границ раздела полупроводника и окисла задаются скоростью поверхностной рекомбинации gS, что определяет величины нормальных к поверхности раздела составляющих плотностей тока Jp и Jn и т. д.
Результат решения уравнений непрерывности и Пуассона при известных краевых условиях — это поля потенциала и концентраций подвижных носителей в различных областях полупроводниковой структуры. Знание этих полей позволяет оценить электрические параметры прибора.
В основе моделей диффузионных процессов, используемых, в частности, для описания технологических операций диффузии примесей при изготовлений интегральных схем и полупроводниковых приборов, лежит уравнение диффузии
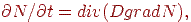
| (15.11) |
где N — концентрация примеси; D — коэффициент диффузии.
Краевые условия представлены зависимостью распределения примеси N в объеме полупроводника в начальный момент времени и зависимостью поверхностной концентрации от времени.
На использовании закономерностей протекания тепловых процессов основано действие многих теплофизических установок. В РЭС полезные свойства обусловлены закономерностями электрических процессов, однако рассеяние мощности и изменения температуры оказывают заметное влияние на характер функционирования аппаратуры. Поэтому в моделях РЭС, как и в моделях многих устройств иной природы, приходится учитывать тепловые процессы. Теплоперенос в твердых телах описывается уравнением теплопроводности
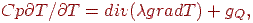
| (15.12) |
где T — температура; С — удельная теплоемкость; р — плотность; λ — коэффициент теплопроводности; gQ — количество теплоты, выделяемой в единицу времени в единице объема.
15. Лекция: Разработка математических моделей при проектировании технологии //
//
Дата добавления: 2015-08-21; просмотров: 1034;
