Алгоритм RSA

Криптосистема RSA была разработана в 1977 году и получила название в честь ее создателей: Рона Ривеста(Ron Rivest), Ади Шамира(Adi Shamir) и Леонарда Адлмана(Leonard Adleman). Они воспользовались тем фактом, что нахождение больших простых чисел в вычислительном отношении осуществляется легко, но разложение на множители произведения двух таких чисел практически невыполнимо. Доказано (теорема Рабина), что раскрытие шифра RSA эквивалентно такому разложению. Поэтому для любой длины ключа можно дать нижнюю оценку числа операций для раскрытия шифра, а с учетом производительности современных компьютеров оценить и необходимое на это время. Возможность гарантированно оценить защищенность алгоритма RSA стала одной из причин популярности этой криптосистемы на фоне десятков других схем. Поэтому алгоритм RSA используется в банковских компьютерных сетях, особенно для работы с удаленными клиентами (обслуживание кредитных карточек).

Безопасность RSA основана на трудности разложения на множители больших чисел. Открытый и закрытый ключи являются функциями двух больших (100–200 разрядов или даже больше) простых чисел. Предполагается, что восстановление открытого текста по шифротексту и открытому ключу эквивалентно разложению на множители двух больших чисел.

Для генерации двух ключей используются два больших случайных простых числа pи q. Для максимальной безопасности выбирайте pи q равной длины. Рассчитывается произведение:

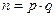
Затем случайным образом выбирается ключ шифрования e, такой что eи 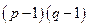являются взаимно простыми числами. Наконец расширенный алгоритм Евклида используется для вычисления ключа дешифрирования d, такого что

Другими словами

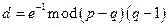
Заметим, что dи nтакже взаимно простые числа. Числа e и n – это открытый ключ, а число d – закрытый. Два простых числа pи q больше не нужны. Они должны быть отброшены, но не должны быть раскрыты.

Для шифрования сообщения m оно сначала разбивается на цифровые блоки, меньшие n(для двоичных данных выбирается самая большая степень числа 2, меньшая n). То есть, если pи q – 100-разрядные простые числа, то nбудет содержать около 200 разрядов, и каждый блок сообщения m_i должен быть около 200 разрядов в длину. (Если нужно зашифровать фиксированное число блоков, их можно дополнить несколькими нулями слева, чтобы гарантировать, что блоки всегда будут меньше n. Зашифрованное сообщение c будет состоять из блоков c_i той же самой длины. Формула шифрования выглядит так

.

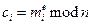Для расшифровки сообщения возьмите каждый зашифрованный блок c_i и вычислите

.

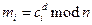Шифрование RSA

Открытый ключ:

n произведение двух простых чисел pи q (pи q должны храниться в секрете)

e число, взаимно простое с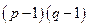

Закрытый ключ:

de^-1mod ((p-1)(q-1))

Шифрование:

c = m^e mod n

Дешифрирование:

m = c^d mod n

Точно также сообщение может быть зашифровано с помощью d, а расшифровано с помощью e, возможен любой выбор.

Короткий пример возможно поможет пояснить работу алгоритма.

Если p= 47 и q= 71, то n= pq= 3337.

Ключ eне должен иметь общих множителей (p-1)(q-1)= 46*70 =3220.

Выберем (случайно) e равным 79. В этом случае d= 79^-1 mod 3220 = 1019.

При вычислении этого числа использован расширенный алгоритм Эвклида. Опубликуем e и n, сохранив в секрете d. Отбросим p и q.

Для шифрования сообщения m = 6882326879666683 сначала разделим его на маленькие блоки. Для нашего случая подойдут трехбуквенные блоки. Сообщение разбивается на шесть блоков m_i:

m_l = 688

m₂= 232

m₃ = 687

m₄= 966

m₅ = 668

m₆ = 003

Первый блок шифруется как 688⁷⁹ mod 3337 = 1570 = c_l.

Выполняя те же операции для последующих блоков, создает шифротекст сообщения:

c = 1570 2756 2091 2276 2423 158.

Для дешифрирования нужно выполнить такое же возведение в степень, используя ключ дешифрирования 1019: 1570¹⁰¹⁹ mod 3337 = 688 = m_l.

Аналогично восстанавливается оставшаяся часть сообщения.