Методы физико-химического анализа и исследования ТП

Поскольку энтропия — величина аддитивная, сумма значений энтропии отдельных АПЕ, составляющих технологическую систе­му, равна энтропии этой системы:

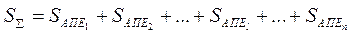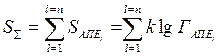или

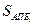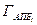где — 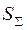энтропия (информационная) технологической системы; , —энтропия отдельной (i-й) АПЕ; п — число АПЕ; —выход годных изделий на отдельной (i-й) АПЕ.

Из анализа данных уравнений следует, что суммарная энтропия ТП может возрастать за счет увеличения энтропии какой-либо одной или нескольких АПЕ, что заставляет исследователя скон­центрировать внимание на изучении этих аппаратурно-процессных единиц.

Предположим, что требуется изменить (улучшить) параметры изделия, т.е. изменить условия его годности. В этом случае при существующем процессе заведомо значение выхода годных будет меньше, а энтропии больше, чем в предыдущем случае. При недо­статочном количестве или полном отсутствии годных изделий по­лучают соответственно большее или равное бесконечности значе­ние энтропии. Следовательно, данный ТП неприемлем для дости­жения поставленных целей.

Лекция №2

Принципы анализа физико-химических процессов технологии ЭС.Методы физической химии позволяют приближенно оценить направление многих процессов при заданных параметрах состоя­ния, а следовательно, и при выбранных режимах ТП. Такой анализ применительно к различным ТП изготовления ЭС рассматриваетсявсоответствующих дисциплинах. Однако при этом часто не принимают во внимание флуктуационные явления. Между тем при изготовлении приборов с микронными, субмикронными и нанометровыми размера­миэлементов флуктуации играют решающую роль. |Во многих процессах, например при получении и травлении тонких пленок, легировании методами диффузии и имплантации, фотолитографии и др., в результате флуктуации технологических режимов (факторов) обработки, а также характеристик обрабаты­вающей среды (растворов, паров, газов, плазмы, лучей и т. п.) появляются статистически распределенные неоднородности свойств обрабатываемой среды, т. е. флуктуации свойств в пределах данно­го микроансамбля (структуры, платы, кристалла и т. п.) Исполь­зуя методы статистической термодинамики, удобно анализировать процессы, протекающие при формировании элементов радиоэлек­тронных устройств микронных и субмикронных размеров.

Основными понятиями статистической термодинамики являют­ся: большой канонический ансамбль, микроканонический ансамбль, фазовое пространство импульсов и координат, энергия. Аналогами этих понятий в технологии РЭА могут служить соответственно генеральная совокупность изделий *, выборка, число степеней сво­боды изменения параметров изделия и технологических факторов ит. п.

Однако есть существенное различие в принципах применения математической статистики к равновесной термодинамике и техно­логии. Если любая термодинамическая система описывается тремя основными параметрами (энергией, импульсом и моментом им­пульса), то в случае технологической системы таких параметров (влияющих факторов) значительно больше. Поэтому статистиче­ский анализ целесообразно применять лишь для исследования флуктуации процесса и воздействий на него. При этом анализ позволяет решить проблемы точности и стабильности (устойчивости) TП.

Как в статистической термодинамике, чтобы начать статистиче­ское описание системы, следует задать ее состояние, так и при ста­тистическом исследовании технологической системы нужно снача­ла выбрать конкретный детерминированный физико-химический процесс, оценить степень его стохастичности и только затем при­ступать к его статистическому описанию и анализу. Фактически такой анализ сводится к исследованию влияния флуктуации техно­логических факторов на распределение параметров качества изде­лий в выбранной совокупности (выборке). При этом технологиче­скими считают термодинамические, кинетические и стохастические факторы. Среди них определяют значащие, незначащие и, главное, доминирующие.

Для поддержания на заданном уровне значений тех или иных влияющих и, особенно, доминирующих технологических факторов разрабатывают системы контроля и управления и на их основе автоматизируют ТП.

Естественно, что автоматизировать управление ТП, в основе ко­торого лежит тот или иной физико-химический процесс, невозмож­но без построения адекватной его математической модели. Резко повысить эффективность анализа физико-химических процессов технологии РЭА можно за счет разработки имитационных моделей, привлекая для работы с такими моделями средства информационно-вычислительной техники. Методика анализа таких моделей постоян­но совершенствуется, разрабатываются автоматизированные си­стемы анализа на базе новейших научных данных, которые ориен­тируются на использование программно-вычислительных возмож­ностей современных ЭВМ.

Анализ физико-химических процессов должен быть причинным, т. е. выявлять причины того или иного явления, отклонений от най­денных ранее закономерностей и т. п. Такой анализ применительно к физико-химическим процессам технологии РЭА только начинает развиваться. Таким образом, физико-химический анализ ТП, по­скольку ТП является большой системой, должен быть системным, т. е. отражать всю совокупность связей между элементами системы (объектами, факторами, параметрами и т. п.).

Важно, чтобы анализ ТП как физико-химической системы осу­ществлялся в динамике, т. е. проявлении функций системы во вре­мени. Поэтому, если равновесная система описывается фазовым пространством состояний, то функционирующую систему можно описать только уравнениями движения в пространстве состояний, что значительно затрудняет анализ ТП по сравнению с классическим физико-химическим анализом. Однако это дает большой простор инженеру-технологу для проявления своего творческого потенциала для повышения эффективности ТП, а, следовательно, и производ­ства в целом.

Основные понятия и способы описания термодинамической и технологической систем

В технологии ЭС используется большое количество процессов, описываемых с помощью термодинамических, кинетических и ста­тистических законов. К таким процессам относятся физическое ифизико-химическое осаждение и растворение слоев, электрохими­ческие, плазменные, диффузионные процессы, создание контактов идр. Большинство технологий построено на процессах, связанных свысокими концентрациями энергий в обрабатываемых материа­лах, особенно в приповерхностных слоях, где формируются рабо­чие элементы ЭС. Это приводит к возникновению неравновесных состояний (напряжений). Электрофизические свойства твердых тел, реализуемых в ЭС, зависят от этих состояний, определяемых типом иконцентрацией дефектов в твердом теле. Большинство электрофизических свойств полуфабрикатов ЭС, аследователь­но, и выход годных изделий зависят от характера сил связей меж­ду атомами в слоях твердого тела и статистического распределения возможных дефектов в структуре этих слоев. Поэтому для анализа исинтеза ТП до описания физико-технологических процессов изготовления ЭС необходимо рас­смотреть основы классической и статистической термодинамики, атакже кинетические закономерности.

Термодинамика как один из основных разделов теорети­ческой физики изучает законы взаимных превращений энергии вравновесных процессах и направление самопроизвольных процес­сов в системе взаимодействующих макро- и микроскопических тел. При установлении основных термодинамических закономерностей, какправило, не детализируются сложные энергетические превра­щения, протекающие внутри тела. Не дифференцируются такжевиды энергии, присущие телу в данном состоянии. Совокупность этих видов энергии рассматривается какединая внутренняя энергия системы.

Положения классической термодинамики не применимы кот­дельным атомам и молекулам, так как для них понятия теплоты иработы теряют смысл. Поэтому в термодинамике анализируют лишь большие ансамбли атомов и молекул, составляющие систе­мы. При этом свойства и поведение отдельных молекул не учиты­вают. Макроскопическую систему, выделяемую в термодинамиче­cкую, в дальнейшем будем называть просто системой. Она имеет определенные границы, отделяющие ее от окружающей среды. Так вот термодинамика в первую очередь изучает физико-химические явления и процессы, сопровождающие энергетическое и материальное взаимодействие системы с внешней средой. Характер этого взаимодействия определяется граничными поверхностями, которые либо непроницаемы для потоков вещества и энергии, либо прозрачны только для энергетических потоков, либо для обоих. В соответствие с этим системы подразделяются на замкнутые, закрытые и открытые (см. рис.1).

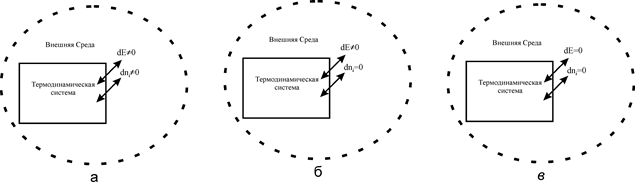
Рис.1. Термодинамические системы:

а-открытые; б-закрытые; в-замкнутые

Открытые системы способны обмениваться веществом и энергией с внешней средой (dE¹0; dn¹0). Большинство реальных систем относится к открытым. В общем случае входящие ы выходящие потоки могут выводить такие системы из термодинамического равновесия и удерживать неопределенно долго в равновесном стационарном состоянии (состоянии текущего равновесия).

В закрытых системах (рис. 1,б) через граничные поверхности возможен лишь энергетический обмен (dE¹0), а массообмен отсутствует (dn=0). Но массы отдельных компонентов внутри системы могут измениться в результате химических реакций внутри системы. Пример космический корабль.

В замкнутых системах (рис. 1,в) полностью отсутствует любой обмен с внешней средой (dE=0; dn=0). Условно эту систему можно смоделировать как идеально термостатированный объект с абсолютно непроницаемыми граничными поверхностями.

Принципиальным отличием замкнутых систем от открытых является поведение во времени. В замкнутых равновесных системах поток любого термодинамического параметра, направленный в одну сторону, компенсируется таким же по значению но направленным противоположно потоком. Можно сказать, что закрытая система инвариантна относительно времени, т.е. дифференциальные уравнения описывающие данные системы инвариантны по отношению к преобразованию
«t» » «-t».

Системы разделяются по виду внутреннего содержания на гомогенные и гетерогенные.

Систему называют гомогенной, если все ее параметры одинако­вы во всех частях или непрерывно меняются от точки к точке.

Систему называют гетерогенной, если она состоит из частей, разделенных видимыми поверхностями раздела. На этих поверх­ностях некоторые параметры системы меняются скачкообразно.

Совокупность отдельных гомогенных частей системы, обладаю­щих одинаковыми свойствами, может условно считаться одной фазой (например, смесь кристаллов одного вещества или совокуп­ность капелек жидкости, взвешенных в газе и составляющих ту­ман, ит. п.).

Состояние и макроскопические свойства любой термодинамической системы полностью и однозначно определяются заданием некоторого числа внутренних параметров, которые называются термодинамическими параметрами состояния.

Исходные термодинамические параметры состояния выбираются произвольно, но, после выбора, все другие переменные оказываются фиксированными. Выбранные переменные, определяющие состояние системы, называются независимыми. Параметры, которые можно выразить через исходные, являются зависимымипеременными.

В отличие от классической химии при термодинамическом описании процессов требуется дополнительные сведения, касающиеся условий их протекания и фазового состояния компонентов.

Например, реакции

2Н_2(g) + О_2(g) = 2H₂O_(g)

2Н_2(g) + О_2(g) = 2H₂O_(l)

из-за различия фазового состава продуктов, (а в нашем случае (g) – газовая фаза, (l) – жидкая фаза)

с позиции термодинамики различны.

В качестве параметров состояния обычно выбирают свойства системы, легко определяемые экспериментально. Параметрами состояния системы в общем случае являются, следующие независимые переменные: темпе­ратура, давление, объем, энтропия, состав (или число молей n), теплота и работа, электрический заряд, площадь поверхности, внешние поля (электрическое, магнитное, гравитационное), интенсивность внешнего излучения и т. д. Соот­ношения, связывающие между собой эти параметры, называют уравнениями состояния системы:

f(p, V, Т, С, С_е, U, S_п) = 0, (1 )

где р — давление; V — объем; Т — температура; С — концентрация компонентов системы; С_е — концентрация носителей заряда; U — электростатический потенциал системы; S_п — площадь поверхности системы. В классической термодинамике рассматривают только равновесные состояния системы, т. е. такие, при которых парамет­ры состояния не изменяются самопроизвольно во времени, а для систем, находящихся в поле внешних сил (например, в электриче­ском или гравитационном), закономерно изменяются от точки к точке в направлении действия поля.

Состояния системы или фазы являются неравновесными, если их параметры (р, V, Т, С, U и др.) изменяются во времени. Нерав­новесные состояния анализируются в термодинамике необратимых процессов.

Основные уравнения классической термодинамики можно выве­сти методами статистической физики (учитывая свойства отдель­ных молекул, составляющих ансамбль), используя математичес­кую статистику. Этот раздел статистической физики называют статистической термодинамикой. Так как в ней определяются как термодинамические состояния, так и кинетические явления, то иобласть ее применения шире области применения классической термодинамики.

Состояние системы можно описать, не анализируя движение каждой частицы, а измеряя, например, ее температуру, объем, давление. Эти величины будут указывать на среднее значение энергии каждого атома.

Некоторые свойства (например Т и р) могут иметь вполне определенные и различные значения в каждой точке системы. Это интенсивные свойства, или интенсивные переменные. Интенсивные переменные не зависят от массы системы и могут изменяться от точки к точке или иметь одно и то же значение во всей системе. Параметры характеризующие систему как единое целое и зависящие от общего количества вещества в системе, называются экстенсивными свойствами, илиэкстенсивными переменными.К экстенсивным свойствам относятся внутренняя энергия, энтропия, свободные энергии Гиббса и Гельмгольца, энтальпия и еще ряд других.

В случае когда основными параметрами состояния выбраны температура и давление, то любое экстенсивное свойство 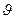будет зависеть не только от Т и р но и от количества каждого из индивидуальных компонентов системы и соотношений меду ними:

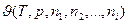(2)

где n₁, n₂, …, n_i – количество молей компонентов системы.

Поскольку экстенсивные величины являются однородными функциями первого порядка по отношению к числу молей и обладают свойством аддитивности, то если увеличивать в 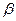раз число частиц каждого сорта в системе, во столько же раз возрастет и значение рассматриваемого экстенсивного свойства:

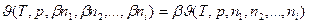. (3)

Частная производная

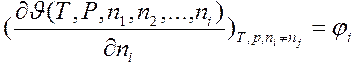(4)

соответствует изменению экстенсивного свойства 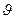системы при добавлении к ней 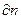молей компонента i и называется парциальной молярной величиной. Эта ведичина характеризует скорость изменения соответствующей функции при изменении числа молей i-го компонента в условиях постоянства температуры и давления.

Из уравнения (4) видно, что для парциальных молярных величин справедливо следующее соотношение:

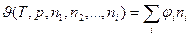. (5)

В дальнейшем мы увидим, что важнейшей парциальной молярной величиной является химический потенциал компонента в смеси.

При математическом описании термодинамических процессов их некоторые комбинации периодически повторяются, что будет проиллюстрировано далее.

Энергия любой термодинамической системы включает в себя следующие основные составляющие:

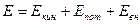, (6)

где 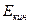-макроскопическая кинетическая энергия системы как единого целого; 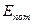- потенциальная энергия системы во внешних силовых полях; 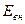- внутренняя энергия системы. Во многих изданиях для обозначения внутренней энергии пользуются буквой U ( прошу не путать с электростатическим потенциалом системы U в формуле (1)).

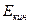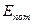Величины и определяются так же, как и в механике.

Внутренняя энергия 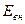зависит от состояния системы и является функцией ее термодинамических параметров.

По определению Р. Клазиуса, внутренняя энергия – это сумма всех видов энегий, которыми обладает система.

В соответствии с характером движения частиц внутри системы основными составляющими внутренней энергии являются энергия массы, кинетическая, вращательная и колебательные энергии частиц, энергия межмолекулярного и внутримолекулярного взаимодействий и др.

На значение внутренней энергии не влияют внешние факторы: перемещение системы в пространстве под действием внешних сил и потенциальная энергия пространственного расположения ее во внешнем силовом поле.

Можно отметить, что абсолютное значение внутренней энергии любой произвольно взятой системы неизвестно и практически не поддается расчету вследствие неопределенности начала отсчета, для которого 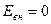. Однако в термодинамике это значение не существенно, а важно лишь изменение 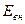при переходе системы из одного состояния в другое.

Внутренняя энергия это сумма средних значений энергий, составляющих систему частиц. Следовательно, она не зависит от промежуточных стадий процесса, а определяется только конечным и начальным состояниями системы и относится к функциям состояния.

Функция состояния – это функция, изменение которой определяется только конечным и начальными состояниями системы и не зависит от пути перехода.

Следовательно, при переходе системы из состояния 1 в состояние 2 изменение ее внутренней энергии можно записать в виде

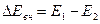, (7)

где 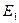, 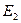- значения внутренней энергии системы соответственно в начальном и конечном состояниях.

Основные соотношения между параметрами термодинамиче­ских систем описываются двумя законами термодинамики.

Первый закон термодинамики (первое начало термодинамики), являясь законом со­хранения энергии, определяет взаимосвязь между теплотой Q, по­глощенной системой, ее внутренней энергией Е_вн и работой А, со­вершаемой системой: при отсутствии материального обмена частицами с внешней средой тепловая энергия, получаемая системой, расходуется на приращение внутренней энергии и совершение работы против сил внешнего давления

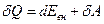(8) (2)

Внутренняя энергия 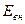является функцией состояния, тогда как подводимая (отводимая) к системе теплота Q и совершаемая работа А не являются таковыми, поскольку зависят от пути перехода системы из состояния с энергией 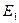в состояние с энергией .

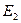В этом уравнении бесконечно малые изменения работы и тепло­ты обозначают через δ, так как 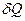и 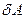не являются полными дифференциалами в отличие от приращения внутренней энергии dE_BH. Это лишний раз подчеркивает, что в отличие от Е_вн теплота и работа характеризуют не системы, а процессы, заключающиеся в передаче энергии в той или иной форме.

В общем случае в (8) должны присутствовать составляющие, учитывающие не только работу, совершаемую по преодолению сил внешнего давления, но и работу, совершаемую против всех остальных сил (электрических, магнитных, и др.), которую принято называть полезной. Тогда для бесконечно малого изменения состояния системы уравнение первого начала термодинамикри примет вид

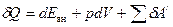, (9)

где 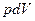- работа по преодолению внешнего давления (работа расширения); 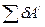- полезная работа против сторонних сил.

Если внутренняя энергия определяется состоянием системы и ее изменение не зависит от характера процесса, т. е. от пути перехода из одного состояния в другое, то теплота и работа зави­сят от способа или формы передачи энергии и их значения зависят от характера процесса. Например, бесконечно малое расширение газа в цилиндре производит работу

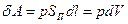(10) (3)

где р— давление газа; S_П — площадь поперечного сечения цилинд­ра; dl — бесконечно малое перемещение поршня; dV — приращение объема газа.

Суммарная работа расширения

(11) (4)

В координатах р — V работа определяется площадью под кри­вой p=f(V), согласно которой система из состояния V₁ переходит в состояние V₂.

Работа равновесного процесса

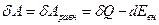(12) (5)

Эта работа максимальна, так как она больше работы любого неравновесного процесса, для которого δA<δQ-dE_вн. Поскольку значения δQ и dЕ_вн равновесного процесса не зависят от пути пе­рехода системы из одного состояния в другое, а определяются только начальным и конечным состояниями системы, и максималь­ная работа также не зависит от пути перехода и определяется лишь начальным и конечным состояниями системы, т. е. является полным дифференциалом.

Второй закон термодинамики вводит новую функцию для описания системы - энтропию. Математически энтропию мож­но представить как:

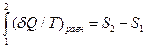(13) (6)

Или

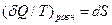(14)

где ( 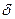Q/T)равн— элементарная приведенная теплота в равновесном¹ процессе; S₂—S₁— приращение некоторой функции состояния сис­темы; dS— дифференциал функции состояния.

Таким образом, интеграл элементарных приведенных теплот в равновесном процессе равен приращению некоторой функции со­стояния системы, а подынтегральное выражение — дифференциалу этой функции.

Итак, энтропия есть функция состояния системы, изменение ко­торой равно сумме приведенных теплот, поглощенных системой в равновесном процессе. Энтропия является однозначной, непрерыв­ной и конечной функцией состояния. Ее выражают в Дж/(К*моль). . Эта единица называется энтропийной единицей.

Перепишем уравнение (12) следующим образом:
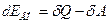(15)

Подставив 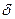А из (10) в (15), получим
dE_m= 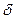Q-pdV. (16)

Тогда с учетом (14) выражение (16) примет вид
dE_BH = TdS — pdV (17)

Таким образом, внутренняя энергия системы может изменяться за счет совершения работы и обмена теплотой.

Для механической системы при стремлении к равновесию ха­рактерно освобождение потенциальной энергии и переход ее в ра­боту, совершаемую над средой. Аналогично этому термодинамическая система при стремлении к равновесию также высвобождает частьвнутренней энергии, которая может передаваться среде в виде теплоты или работы. Эту составляющую внутренней энергии назы­вают свободной энергией G.

Свободную энергию термодинамической системы, так же как и внутреннюю, можно разбить на тепловую и потенциальную состав­ляющие. Тепловая составляющая зависит от степени упорядочен­ности теплового движения частиц, а потенциальная определяется силовым взаимодействием атомов без учета их теплового движе­ния. Взаимосвязь между тепловой и потенциальной составляющи­ми свободной энергии лежит в основе ряда физических явлений и превращений.

Так как изменение свободной энергии определяется только раз­ностью состояний системы и не зависит от пути перехода из одного состояния в другое, то оно является полным дифференциалом от параметров состояния системы:

 

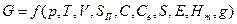где E — электрический потенциал; Н_т—магнитный потенциалу g — гравитационный потенциал.

Для упрощения записи обозначим параметры состояния следующим образом:

 

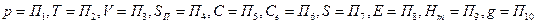
Если параметры состояния термодинамической системы извест­ны, то систему можно описать уравнением вида

 

 

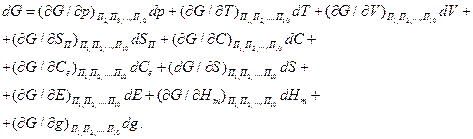(18)

 

Так как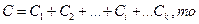

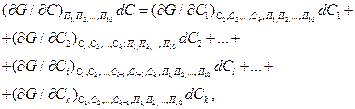
где k — число компонентов.

Члены уравнения (18) могут быть представлены в виде

 

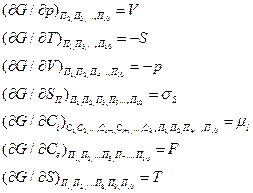(19)

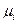и т. д.

где 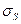— поверхностная энергия; — химический потенциал i-гo компонента; F — уровень Ферми.

В общем случае движущей силой процесса является градиент свободной энергии по тому параметру состояния П, который пере­носится в процессе. Поэтому dG/дПназывают параметрическим потенциалом и обозначают П_i. Если П — концентрация компонен­та i,то Пi— его химический потенциал 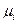; если П— площадь по­верхности, то Пi— поверхностная энергия и т. д.

В дальнейшем рассмотрим отдельные составляющие уравнения (19),способы их определения расчетным или экспериментальным путем, а также их вклад в физико-технологические характеристи­ки процессов, используемых при изготовлении ЭС.

Далеко не для всех технологических систем нужно знать все параметры состояния. Достаточно знать лишь те из них, которые оказывают существенное влияние на изменение свободной энергии данного процесса. Если для конкретной термодинамической систе­мы некоторые параметры состояния можно признать незначащими, то уравнение (18)можно значительно упростить. Так, в отсутст­вие электрического, магнитного и гравитационного полей изменение свободной энергии

dG = Vdp - SdT - pdV + TdS. (20)

Часть свободной энергии системы, которая может превращать­ся в работу, является функцией состояния системы:

dG_H = -SdT - pdV. (14)

Функцию G_H называют свободной энергией Гельмгольца.

Аналогично, когда кроме работы расширения имеют место дру­гие виды работы, соответствующую функцию состояния можно за­писать как

dG_G = -SdT +Vdp. (15)

Функцию G_Gназывают свободной энергией Гиббса. При вычис­лении свободной энергии часто используют функцию состояния, называемую теплосодержанием или энтальпией:

dH = TdS+Vdp. (16)

Эта функция Нчисленно равна количеству теплоты, выделяемой или поглощаемой системой в данном процессе при постоянном давлении.

Связь между свободной энергией Гельмгольца и внутренней энергией определяется уравнением

G_H=E_вн-TS, (17)

связь между свободной энергией Гиббса и энтальпией — уравне­нием

G_g= H-TS. (18)

Однако в выражениях (17)и (18)связь между указанными величинами не является явной, поскольку в них входит энтропия S,которая является термодинамической функцией состояния.

Подставив соотношения

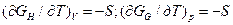(19)

в (17) и (18), получим

G_H = E_BН + T(дG_H/dT)_v; (20)

G_Q=H +T(дG_G/dT)_p. (21)

Уравнения (20) и (21) называют уравнениями Гиббса — Гельмгольца. Они имеют важное значение в практике термодина­мических расчетов. Приведенные функции состояния (Е_вн, G_H, G_G, Н),через производные которых просто и в явном виде могут быть выражены все термодинамические свойства системы, называют характеристическими функциями или термодинамическими по­тенциалами.

Из соотношений (10), (14) — (16) следует, что систему могут характеризовать не только функции Е_вн, G_H, G_G, Н,но и параметры состояния Т, р, S, V,если их выразить через характе­ристические функции, например, T=f(G_H, V);p=f(G_G, Т);S =f(H,р); V=f(Е_bh,S).Этот вывод важен для инженерной прак­тики, так как позволяет пользоваться для анализа и расчета про­цессов привычными величинами: р, V, Ти S.