Другие распределения
| Название | Уравнение | Особенности | Примеры |
| Хи-квадрат | 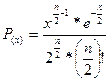
| Таблицы распределения задаются в виде процентных точек, задаваемых условием 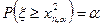
| Используется при построении доверительных интервалов для оценок дисперсии. |
| Стьюдента | 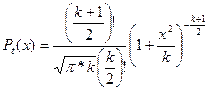 ,
k=n-1, ,
k=n-1, 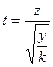
| Так распределена СВ, t, где z- распределено нормально ( 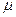 =0, =0, 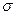 =1); y- имеет распределение хи-квадрат с k степенями свободы =1); y- имеет распределение хи-квадрат с k степенями свободы
| Используется при определении доверительных интервалов среднего арифметического при экспериментально оцениваемой дисперсии. |
| Фишера | 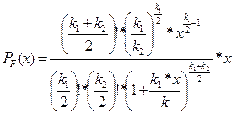 , , 
| Так распределена СВ 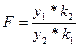 ,где ,где  -имеют распределение хи- квадрат с -имеют распределение хи- квадрат с 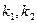 степенями свободы соответственно. степенями свободы соответственно. 
| Используется при дисперсионном анализе |
| Рэлея | 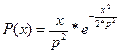 , ,
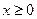
| Имеет модуль двумерного вектора, координаты которого распределены нормально с нулевым средним и равными 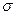
| Для аппроксимации распределения контролируемых показателей, которые могут быть только одного знака. |
| Равномерное | 
| Имеет погрешность округления | Обладает наибольшей неопределенностью для всех СВ, принимающих значение в интервале (a-b;a+b). Во многих случаях может рассматриваться как крайний случай, как наихудшее распределение. |
| Арккоси-нусное | 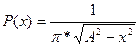 , ,
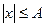
| Такое распределение имеют отсчеты гармонического колебания с равномерно распределенной начальной фазой. Также значения контролируемых параметров, которые в процессе изготовления подвергаются регулированию. |
Критерии и алгоритмы обнаружения глобального экстремума при распознавании распределения Пуассона(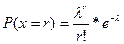 ). Функция имеет глобальное решение при
). Функция имеет глобальное решение при 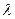 > 0. Расчет критерия оптимизации U =
> 0. Расчет критерия оптимизации U = 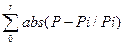
Алгоритм расчета 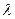
|
| 1. База данных эксперимента (xi, Pi) |
2. Оценка 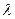 по xi = max. по xi = max.
|
| 3. Расчет факториала при заданном r |
4. Поиск решения значения 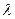 аналогично п. 4- 9 таблицы 6 аналогично п. 4- 9 таблицы 6
|
Нельзя задавать значение r большей экспериментальной.
Критерии и алгоритмы обнаружения глобального экстремума при распознавании распределения Коши(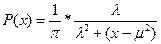 ). Функция имеет глобальное решение при
). Функция имеет глобальное решение при 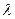 > 0. Расчет критерия оптимизации U =
> 0. Расчет критерия оптимизации U = 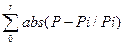
Алгоритм расчета 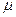 и и 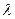
|
| 1. База данных эксперимента (xi, Pi) |
2. Оценка 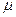 по xi = max. по xi = max.
|
2. Оценка 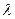 по «полуширине» экспериментальной функции распределения. В случае если теоретическая кривая с оцененными значениями по «полуширине» экспериментальной функции распределения. В случае если теоретическая кривая с оцененными значениями 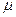 и и 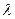 выше экспериментальной, то выше экспериментальной, то 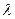 дополнительно умножается на коэффициент более 1 (обычно на 6) дополнительно умножается на коэффициент более 1 (обычно на 6)
|
3. Поиск решения при совместном переборе значений 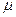 и и 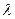 аналогично п. 4- 9 таблицы 6 аналогично п. 4- 9 таблицы 6
|
Дата добавления: 2015-08-21; просмотров: 680;
