Образование и задание поверхности на чертеже.

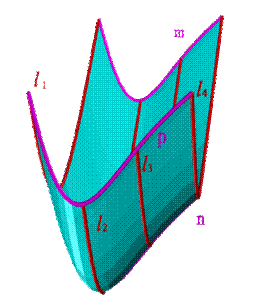
Поверхность можно рассматривать, как совокупность последовательных положений l₁,l₂… линии l, перемещающейся в пространстве по определенному закону (рис.8.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму - изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в одной линии или целого семейства линий (m, n, p...). Подвижную линию принято называть образующей, неподвижные - направляющими. Такой способ образования поверхности принято называть кинематическим.

	Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несет на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество, линий конгруэнтных профилю резца. По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая. Линейчатые поверхности в свою очередь разделяют на так называемые развертывающие, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся. Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Это так называемые циклические поверхности (рис.8.2). Если же группировать поверхности по закону движения образующей линии и производящей поверхности, то большинство встречающихся в технике поверхностей можно разделить на: ·Поверхности вращения; ·Винтовые поверхности; ·Поверхности с плоскостью параллелизма; ·Поверхности переноса. Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают ее форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов). Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности. Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом. Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже. Различают две части определителя: геометрическую и алгоритмическую. Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности. Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу. Например, циклическая поверхность, каркас которой состоит из окружностей (рис.8.3), может быть задан следующим образом: ·Геометрическая часть определителя: три направляющих l, m, n, ось iпучка плоскостей ·Алгоритмическая часть: выделяем из пучка плоскостей с осью i плоскость α; находим точки А, В, С, в которых αпересекает соответственно направляющие l, m, n. Строим окружность, определяемую тремя найденными точками. Переходим к следующей плоскости пучка и повторяем построение.
Рисунок 8.1. Поверхность образованная движением линии
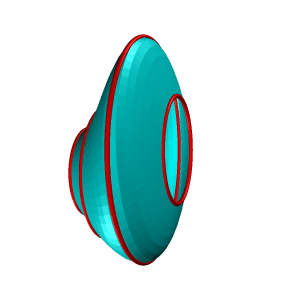
Рисунок 8.2. Циклическая поверхность
Рисунок 8.3. Образование циклической поверхности

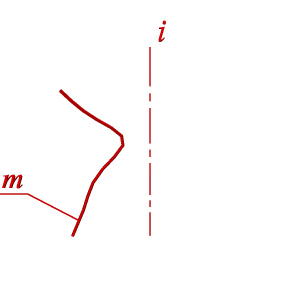
Поверхности вращения – это поверхности созданные при вращении образующей mвокруг оси i (рис.8.4).

Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис 8.4.а).

Алгоритмическая часть включает две операции:

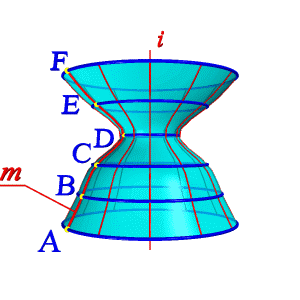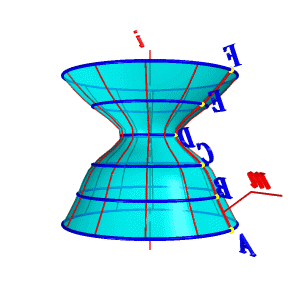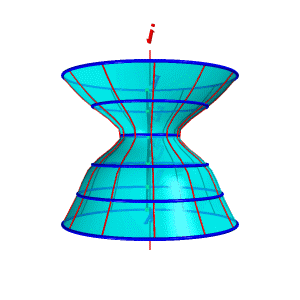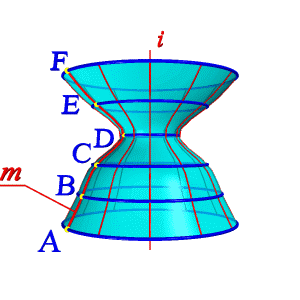
1. На образующей mвыделяют ряд точек A, B, C,…F;

2. Каждую точку вращают вокруг оси i.

а) эпюр		б) модель
Рисунок 8.4. Образование поверхности вращения

Так создается каркас поверхности, состоящей из множества окружностей (рис.8.5), плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Из закона образования поверхности вращения вытекают два основных свойства: 1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели. 2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам. Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.

Рисунок 8.5 Поверхность вращения

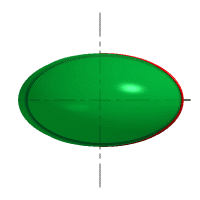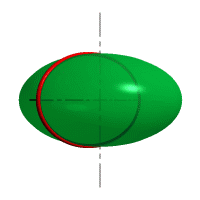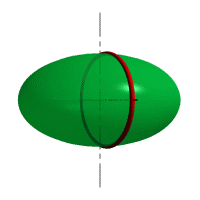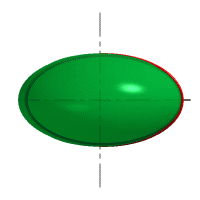
	Рисунок 8.6. Образование сферы	Рисунок 8.7. Образование сфероида

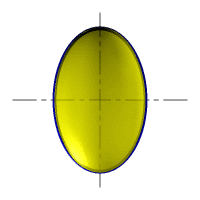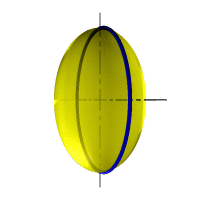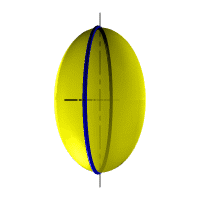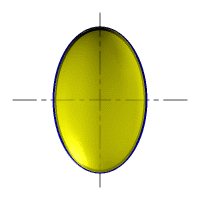
Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими: Сфера – образуется вращением окружности вокруг её диаметра (рис.8.6). При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг большой оси то эллипсоид называется вытянутым (рис.8.8), если вокруг малой – сжатым или сфероидом (рис.8.7). Тор – поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.8.9). Параболоид вращения – образуется при вращении параболы вокруг своей оси (рис.8.10).

Рисунок 8.8. Образование вытянутого эллипсоида

Рисунок 8.8. Тор	Рисунок 8.10. Параболоид вращения

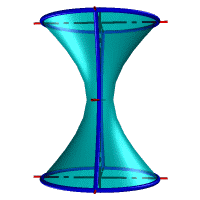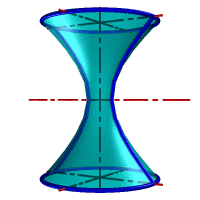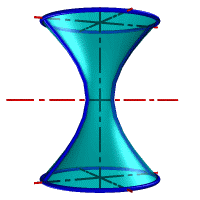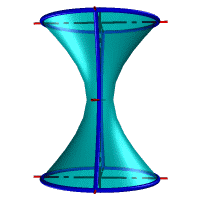
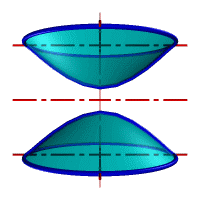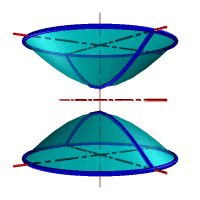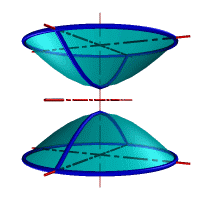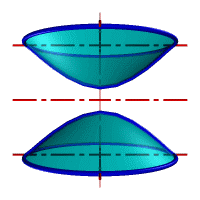
а) однополостной	б) двуполостной
Рисунок 8.11. Гиперболоид вращения

Гиперболоид вращения– различают одно (рис.8.11а) и двух (рис.8.11б) полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.