Энтропия. Энергия Гиббса
Для описания состояния системы, состоящей из большого количества мельчайших частиц (атомов, молекул и др.), необходимо учитывать количество микросостояний (W), посредством которых может быть реализована данная система. Так как количество микросостояний имеет большую величину, на практике пользуются её логарифмом. Эту величину называют энтропией и обозначают S. Отсюда:
| S = k·lgW | (8.4) |
где k – коэффициент пропорциональности (постоянная Больцмана),
W – число микросостояний, соответствующих данной системе.
Энтропия также является функцией состояния, её размерность 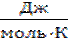 .
.
В изолированной системе самопроизвольно могут протекать только такие реакции или фазовые переходы, которые ведут к увеличению неупорядоченноности системы, т.е. к увеличению энтропии, поэтому энтропию часто определяют как меру беспорядка системы.
В отличие от внутренней энергии и энтальпии для энтропии известны абсолютные значения. Это стало возможным благодаря постулату Планка – энтропия любого простого вещества при 0 К принята условно равной нулю.
При повышении температуры энтропия возрастает. В общем виде зависимость S от Т приведена на рисунке 8.1 из которого видно, что в случае фазовых переходов (плавление, кипение, конденсация и т.д.) изменение энтропии происходит скачкообразно. Изменение энтропии при стандартных условиях обозначается ΔS0298. Для простых веществ ΔS0298 будет больше 0.
Рисунок 8.1 Изменение энтропии при нагревании
Движущая сила процесса складывается из двух сил: стремления к упорядочению (DН) и стремления к беспорядку (TDS). При p и T = const общую дви-
жущую силу процесса называют изобарно-изотермическим потенциалом или энергией Гиббса (DG) и вычисляют по формуле
| DG = DH - TDS. | (8.5) |
При стандартных условиях энергия Гиббса обозначается ΔG0298. Энергия Гиббса также является функцией состояния, поэтому для расчетов её можно применять закон Гесса и его следствия. Вычислив изменение DG в ходе процесса, можно сделать следующие выводы:
DG < 0 – самопроизвольно протекает прямой процесс,
DG > 0 – самопроизвольно протекает обратный процесс,
DG = 0 – состояние равновесия.
При p и T = const общую движущую силу процесса называется изохорно-изотермическим потенциалом или энергией Гельмгольца (DF)
| D F= DU - TDS. | (8.6) |
Термодинамические величины (U, Н, S, G, F) являются функциями состояния, поэтому изменение их в ходе процесса можно вычислить, используя закон Гесса и его следствия. При решении задач следует учитывать, что, как правило, ΔU, DН, DG и DF выражают в кДж, а S– в Дж/К.
Дата добавления: 2015-08-21; просмотров: 1465;
