Кинематика автомобильного дифференциала
При помощи дифференциального механизма (рис.6.6) в автомобилях осуществляется передача вращательного движения от двигателя к ведущим колёсам. При повороте дифференциальный механизм распределяет мощности между ведущими колёсами таким образом, чтобы их обороты согласовывались с условиями движения.
Дифференциальный механизм состоит из центральных конических колёс 3 и 4, конического колеса – сателлита 5 и водила 2. Водило выполнено в виде конического колеса и передача вращения водилу осуществляется от карданного вала 1 при помощи обычной конической передачи 1 – 2. На основании (6.2):
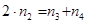(6.4)
Формула (6.4) связывает обороты водила n2 и обороты левого и правого колёс. Число оборотов n2 является известным. Если машина движется прямолинейно, то равенству к (6.4) добавляется n3=n4. При повороте к равенству (6.4) добавляется:
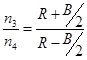(6.5)
Равенство (6.4) и (6.5) позволяют получить определённость решения и найти n3 и n4 .
Рис.6.6
Планетарные механизмы
Если у дифференциального механизма центральное колесо 1 сделать неподвижным и тем самым отнять одну степень подвижности, то можно получить зубчатый механизм с одной степенью подвижности (рис.6.7).
Зубчатые механизмы со степенью подвижности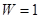 
, у которых геометрические оси некоторых колёс перемещаются, называются планетарными механизмами.
Найдём передаточные отношения. Рассматривая планетарный механизм как частный случай дифференциального механизма и полагая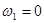 
, можно применить формулу (6.3). Получим:
= 
.
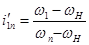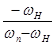Обратное передаточное отношение
,
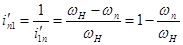где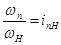 
- передаточное отношение от вала любого колеса n к валу водила H.
Следовательно,
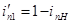или 
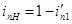(6.6)
Отметим, что к формуле (6.6) под цифрой 1 обозначено неподвижное колесо. Это необходимо учитывать и корректировать формулу при решении задач.
Рис.6.7
Дата добавления: 2015-08-21; просмотров: 705;