К определению оптимальных настроек регуляторов при детерминированных воздействиях и низкочастотных помехах
Рассмотрим замкнутую АСР, представленную на рис. 2.22а. На объект действуют помехи fi по каналам, передаточные функции которых обозначены как Wni(p).
Высокочастотные помехи подавляются самим объектом, а влияние низкочастотных будем стремиться уменьшить за счет оптимальной настройки регулятора. Кроме того, будем считать, что промежуточные помехи в АСР не имеют места.
Передаточные функции системы по управляющему воздействию и помехам запишутся соответственно
 (2.62)
(2.62)
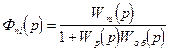 , (2.63)
, (2.63)
а изображение выходного сигнала АСР
 (2.64)
(2.64)
Преобразуем нашу систему (см. рис. 2.22б) таким образом, чтобы помеха была введена на вход системы через соответствующий фильтр с передаточной функцией [12] :
Vni(p)
Для эквивалентности система Vni(p) должна быть связана с передаточными функциями исходной системы выражением
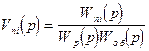 (2.65)
(2.65)
Чтобы помеха не сказывалась на работе АСР достаточно, чтобы она не пропускалась фильтром Vni(p).
Воспользуемся разложением амплитудно-частотных характеристик АСР по управляющему воздействию и фильтра помех в ряд Тейлора вблизи нулевой частоты :
 (2.66)
(2.66)
 (2.67)
(2.67)
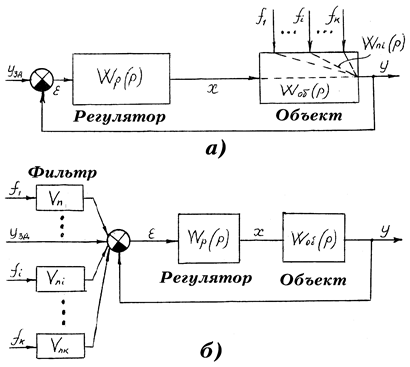
Рис. 2.22 – К определению оптимальных настроек регуляторов при детерминированных воздействиях и низкочастотных помехах:
а - исходная схема; б - преобразованная схема
Для обеспечения наилучшего подавления в системе низкочастотных помех и наилучшего пропускания управляющего сигнала необходимо добиться за счет соответствующей настройки регулятора выполнения следующих условий:
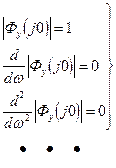 (2.68а)
(2.68а) 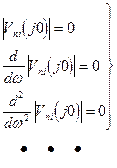 (2.68б)
(2.68б)
Чем больше число коэффициентов разложения обращается в нуль, тем лучше подавляются низкочастотные помехи.
Перейдем к конкретному рассмотрению нахождения оптимальных настроек регулятора из системы уравнений (2.68).
Для системы с ПИД-регулятором АЧХ фильтра для некоторой i -ой помехи определяются формулой:
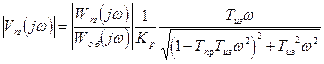 (2.69)
(2.69)
Производные от этого выражения при =0 принимают значения:
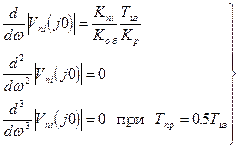 , (2.70)
, (2.70)
где Kni - коэффициент передачи по 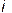 -му каналу помехи. Сама АЧХ при =0 по выражению (2.69б) равна нулю. Дальнейшие вычисления производных дают те же значения, что и вычисленные первые три. Выражения (2.68а) при =0 выполняются.
-му каналу помехи. Сама АЧХ при =0 по выражению (2.69б) равна нулю. Дальнейшие вычисления производных дают те же значения, что и вычисленные первые три. Выражения (2.68а) при =0 выполняются.
Таким образом, при оптимальной настойке регулятора необходимо иметь максимально возможную величину отношения коэффициента передачи регулятора Kp ко времени изодрома Tиз , так как при этом :
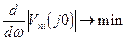
Кроме того, время предварения регулятора должно быть однозначно связано с величиной времени изодрома и составлять половину последнего.
Выражение для АЧХ фильтра для произвольной i -ой помехи в системе с ПИ-регулятором получим, полагая в (2.69) Tпр=0:
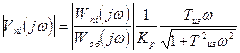 (2.71)
(2.71)
При ω=0 это выражение обращается в нуль. Первая производная от (2.71) при ω=0 принимает значение:
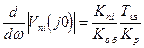 , (2.72)
, (2.72)
т.е. наилучшему подавлению низкочастотных помех соответствует максимум отношения Kp/Tиз.
Аналогично, для системы с ПД-регулятором, полагая в (2.69) 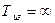 получаем:
получаем:
 , (2.73)
, (2.73)
а
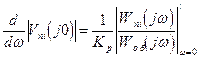 (2.74)
(2.74)
Оба выражения при ω=0 стремятся к нулю при беспредельном увеличении коэффициента передачи регулятора Kp.
Для системы с П-регулятором:
 (2.75)
(2.75)
При ω=0 выражение принимает значение
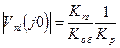 (2.76)
(2.76)
Для наилучшей фильтрации помех следует стремиться к возможно большему Kp.
Наконец, для системы с И-регулятором:
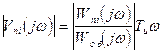 (2.77)
(2.77)
При ω=0 АЧХ фильтра обращается в нуль. Выражение для первой производной при нулевой частоте имеет значение:
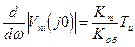 (2.78)
(2.78)
Из (2.77) и (2.78) следует, что наилучшая фильтрация низкочастотных помех имеет место при 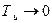 .
.
Как будет показано ниже расчет АСР с астатическими регуляторами (И, ПИ, ПИД) может быть преобразован к расчету АСР с П- или ПД-регулятором, путем отнесения полинома знаменателя регулятора к объекту регулирования, а общий коэффициент усиления системы может быть представлен выражением
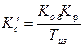 для ПИ- и ПИД-регуляторов (2.79а)
для ПИ- и ПИД-регуляторов (2.79а)
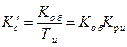 для И-регулятора (2.79б)
для И-регулятора (2.79б)
Тогда из выражений (2.70), (2.72), (2.78) следует, что оптимальные настройки астатических регуляторов сводятся к получению максимального коэффициента усиления K’c преобразованной системы, согласно (2.79), а для П- и ПД-регуляторов- к получению максимума Kc, соответствующего выражению:
Kc= KобKp (2.80)
Так как в пределе K’c и Kc могут быть увеличены до Kкр соответствующей системы, то отсюда целесообразно выбрать в качестве критерия оптимальности критерий Kкр, который следует максимизировать.
Дата добавления: 2015-08-21; просмотров: 660;
