Інтегруваня за частинами в невласному інтегралі І роду

Теорема 4. Нехай функції 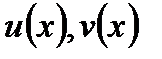визначені ідиференційовані на 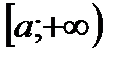, при цьому виконуються наступні умови:

1) Функції 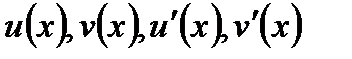- неперервні на ;

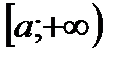2) ;

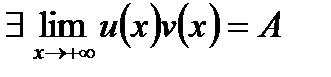3) ,

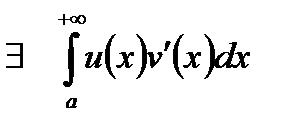тоді

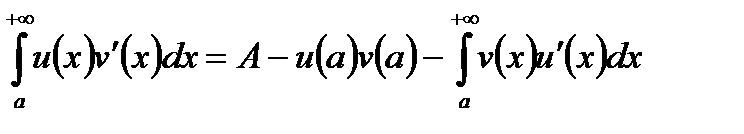. (1)

Формула (1) називається формулою інтегрування за частинами в НІ І роду.

Доказ. Розглянемо будь-який 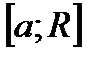. На ньому діє знайома формула інтегрування за частинами для інтегралу Рімана:

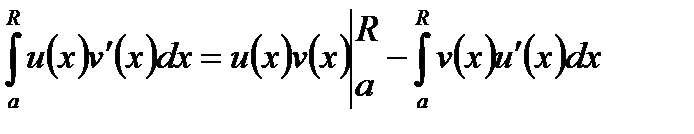. (2)

З умов теореми маємо, що

.

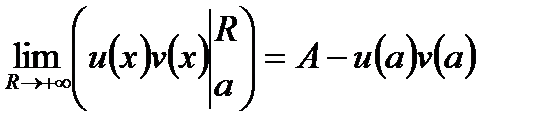Тоді з рівняння (2) витікає одночасна збіжність чи розбіжність інтегралів 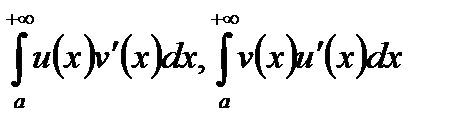, і має місце (1), коли один з інтегралів збігається.

Визначення 2. Невласний інтеграл І роду також можна визначити наступним чином:

,

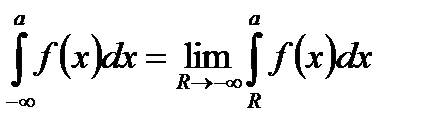чи

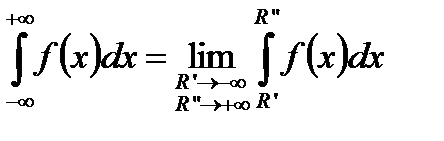, (3)

до того ж в (3) 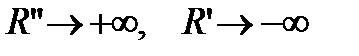незалежно одне від одного.

Питання

1. Коли НІ І роду називається абсолютно збіжним? Навести приклади абсолютно збіжних НІ І роду.

2. Коли НІ І роду називається умовно збіжним? Навести приклади умовно збіжних НІ І роду.

3. Як повязані між собою абсолютна і умовна збіжність НІ І роду?

4. Ознаки Абеля та Діріхлє.

5. При яких умовах можна проводити заміну змінної у НІ І роду? Навести приклади.

6. Коли у НІ І роду можна проводити інтегрування за частинами? Навести приклади.