Заміна змінної в невласному інтегралі І роду

План

1. Абсолютна і умовна збіжність невласного інтегралу І роду
2. Заміна змінної в невласному інтегралі І роду
3. Інтегруваня за частинами в невласному інтегралі І роду

1.Абсолютна і умовна збіжність невласного інтегралу І роду

Визначення 1 . НІ І роду 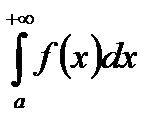збігається абсолютно, якщо збігається .

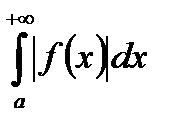Якщо 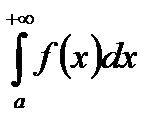збігається , а 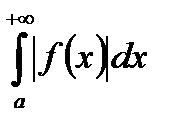розбігається, то кажуть, що 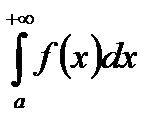збігається умовно.

Твердження. З абсолютної збіжності невластивого інтегралу витікає його збіжність.

Доведення витікає з загальної достатньої умови збіжності (лекція 37), якщо покласти .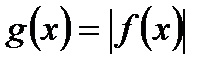

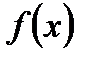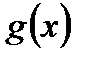Теорема 1 (ознака Абеля). Нехай і визначені на 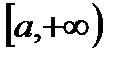і виконуються наступні умови:

1) 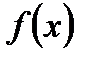інтегрована на 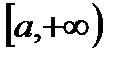, тобто 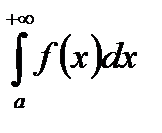є збіжним;

2) 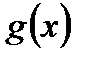- монотонна і обмежена на ,

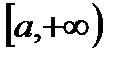тоді 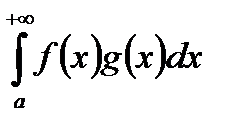збігається.

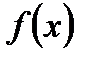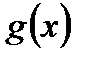Теорема 2 (ознака Діріхлє). Нехай і визначені на 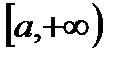і виконуються наступні умови:

1) для 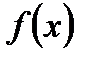функція 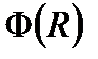, яка визначається як 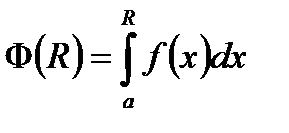, є обмеженою на множині ;

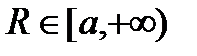2) 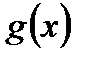монотонна функція на , ,

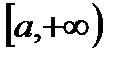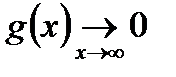тоді 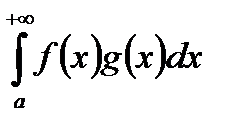збігається.

Зауваження. З ознаки Діріхлє витікає ознака Абеля.

Доказ. Покажемо, що висновки, які робляться з теореми Абеля, витікають з умов Діріхлє.

1) В теоремі Абеля для функції 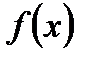вимагається збіжність 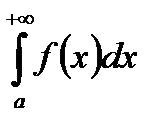. Інтеграл 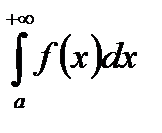збіжний, якщо існує 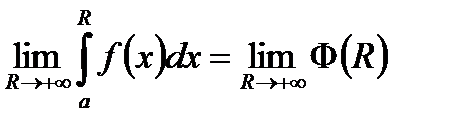. З існування границі функції 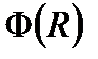витікає її обмеженість. Таким чином, виконується перша умова ознаки Діріхлє.

2) В ознаці Абеля функція 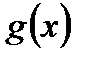повинна бути монотонною і обмеженою. З цього витікає існування скінченної границі 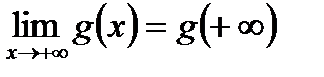. Враховуючи це, розглянемо :

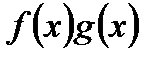Таким чином, маючи умови ознаки Абеля, які накладаються на функці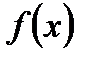ї і 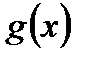, ми можемо довести збіжність 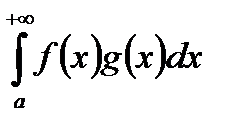, користуючись ознакою Діріхлє, що й потрібно було довести.

Приклад. Дослідити на збіжність .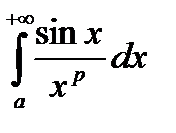

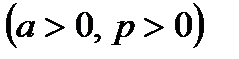Покажемо виконання умов Діріхлє для підінтегральної функції. Для цього оберемо:

, .

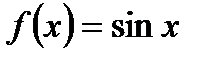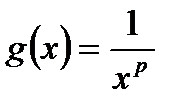Такий вибір є доцільним, оскільки для обраних функцій виконуються умови Діріхлє. Дійсно:

,

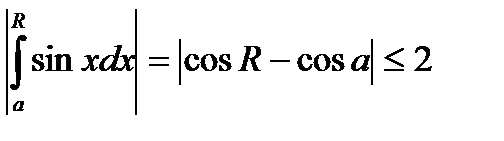що говоре про виконання 1) умови для функції ;

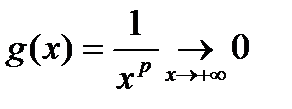, якщо 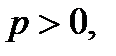до того ж 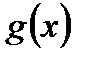монотонна,

що свідчить про виконання умови 2). Тому 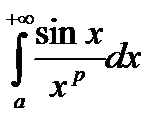збігається при .

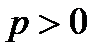Заміна змінної в невласному інтегралі І роду

Теорема 3. Нехай функція 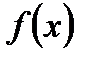визначена на 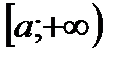, і для неї виконуються наступні умови:

1) 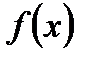неперервна на ;

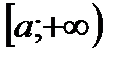2) 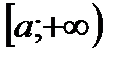є областю значень деякої строго монотонної функції 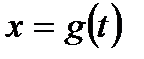, 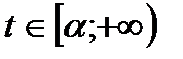(а можливо );

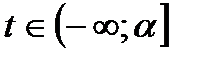3) 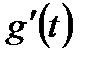- неперервна на 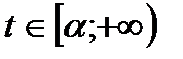(чи );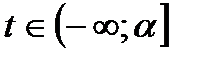

4) ,

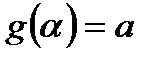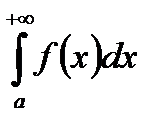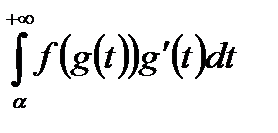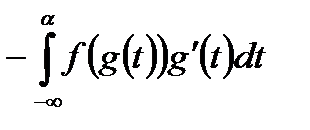тоді збіжність (розбіжність) рівносильна збіжності (розбіжності) (чи ) і

.

Доказ витікає з розглядання звичайного інтегралу Римана 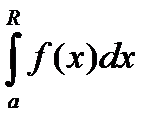, в якому робимо заміну змінною, а потім переходимо до границі, коли .

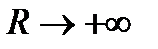Приклад. Обчислити інтеграл 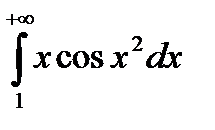чи довести його розбіжність.

.

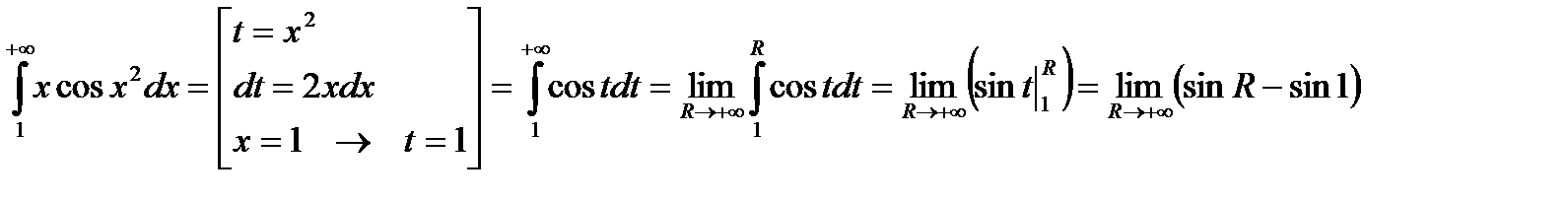Отримана границя не існує, тому поданий інтеграл є розбіжним.