Замена переменной в несобственном интеграле І рода

План

1. Абсолютная и условная сходимость несобственного интеграла І рода
2. Замена переменной в несобственном интеграле І рода
3. Інтегрирование по частям в несобственном интеграле І рода

1. Абсолютная и условная сходимость несобственного интеграла І рода

Определение 1 . НИ І рода 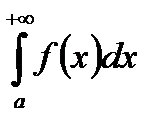сходится абсолютно, если сходится .

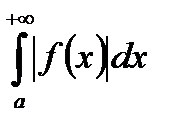Если 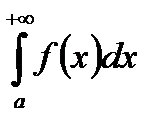сходится, а 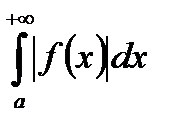расходится, то говорят, что 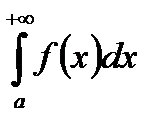сходится условно.

Утверждение. Из абсолютной сходимости несобственного интеграла вытекает его сходимость.

Доказательство вытекает из общего достаточного условия сходимости (лекция 37), если положить .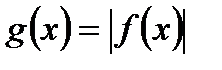

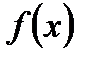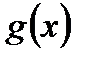Теорема 1 (признак Абеля). Пусть и определены на 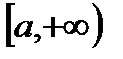и выполняются следующие условия:

1) 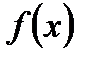интегрируема на 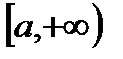, т.е. 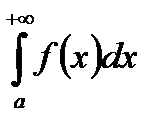является сходящимся;

2) 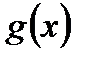- монотонна и ограничена на ,

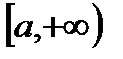тогда 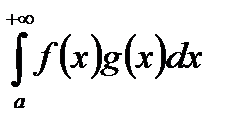сходится.

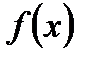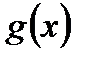Теорема 2 (признак Дирихле). Пусть и определены на 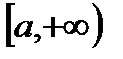и выполняются следующие условия:

1) для 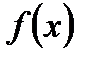функция 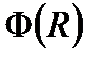, которая определяется как 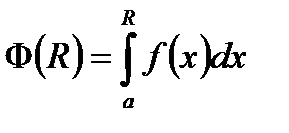, является ограниченной на множестве ;

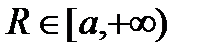2) 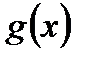монотонная функция на , ,

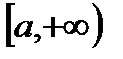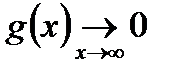тогда 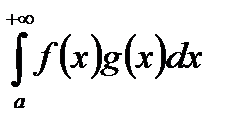сходится.

Замечание. Из признака Дирихле вытекает признак Абеля.

Доказательство. Покажем, что выводы, которые делаются из теоремы Абеля, вытекают из условий Дирихле.

1) В теореме Абеля для функции 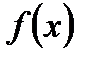требуется сходимость 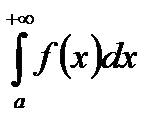. Интеграл 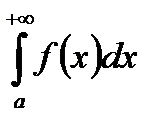сходящийся, если существует 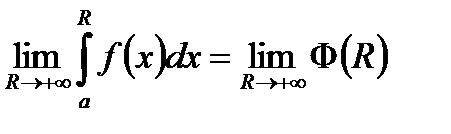. Из существования предела функции 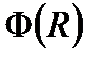вытекает ее ограниченность. Таким образом, выполняется первое условие признака Дирихле.

2) В признаке Абеля функция 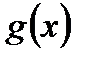должна быть монотонной и ограниченной. Из этого вытекает существование конечного предела 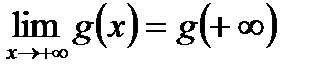. Учитывая это, рассмотрим :

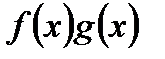Таким образом, имея условия признака Абеля, которые накладываются на функци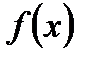и и 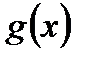, мы можем доказать сходимость 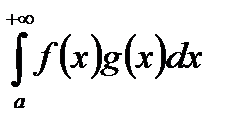, пользуясь признаком Дирихле, что и нужно было доказать.

Пример. Исследовать на сходимость .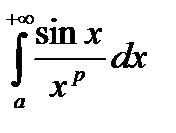

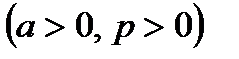Покажем выполнение условий Дирихле для подинтегральной функции. Для этого выберем:

, .

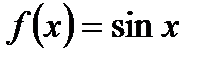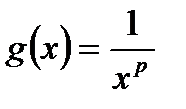Такой выбор является целесообразным, поскольку для выбранных функций выполняются условия Дирихле. Действительно:

,

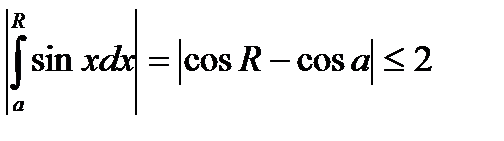что говорит о выполнении 1) условия для функции ;

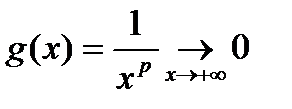, если 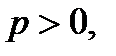к тому же 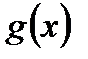монотонная,

что свидетельствует о выполнении условия 2). Поэтому 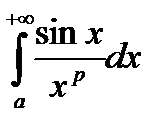сходится при .

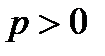Замена переменной в несобственном интеграле І рода

Теорема 3. Пусть функция 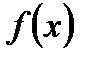определена на 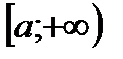, и для нее выполняются следующие условия:

1) 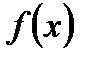непрерывна на ;

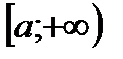2) 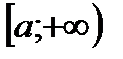является областью значений некоторой строго монотонной функции 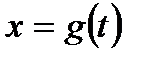, 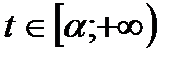(а возможно );

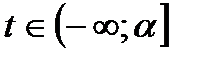3) 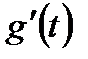- непрерывна на 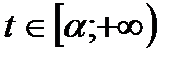(или );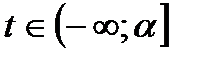

4) ,

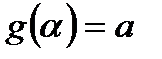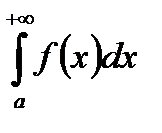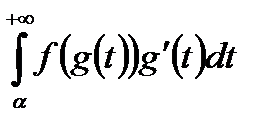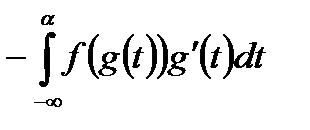тогда сходимость (расходимость) равносильна сходимости (расходимости) (или ) и

.

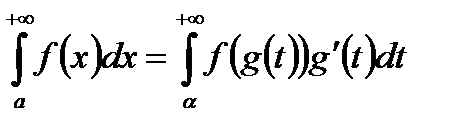Доказательство вытекает из рассмотрения обычного интеграла Римана 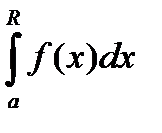, в котором делаем замену переменной, а потом переходим к пределу, когда .

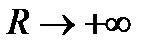Пример. Обчислити інтеграл 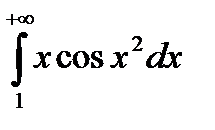чи довести його розбіжність.

.

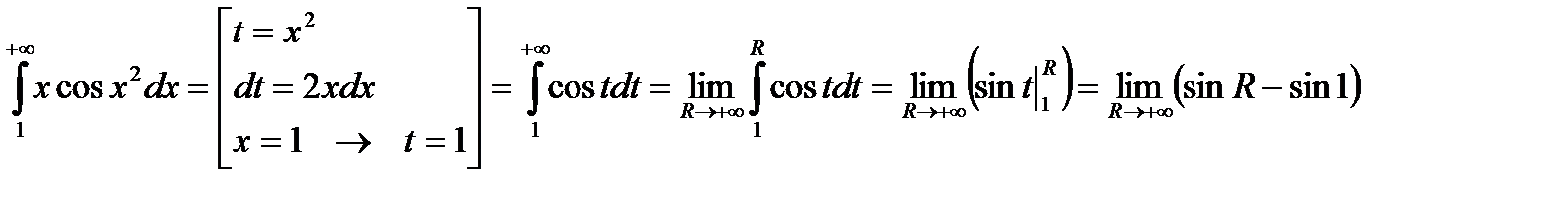Отримана границя не існує, тому поданий інтеграл є розбіжним.