Второе и третье достаточные условия локального экстремума
Теорема 2 (второе достаточное условие локального экстремума). Пусть функция  определена на
определена на 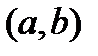 ,
, 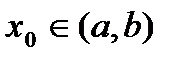 , и выполняются условия:
, и выполняются условия:
1. 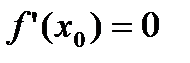 ;
;
2. существует 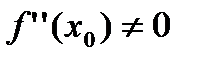 ,
,
тогда  имеет локальный экстремум в точке
имеет локальный экстремум в точке 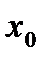 , а именно
, а именно
- локальный максимум, если 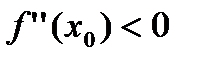 ;
;
- локальный минимум, если 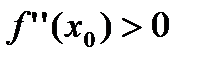 .
.
Второе достаточное условие является частным случаем третьего достаточного условия локального экстремума.
Пусть функция  определена на
определена на 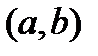 и
и 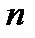 раз дифференцирована в точке
раз дифференцирована в точке 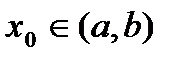 , и выполняются условия:
, и выполняются условия:
 ,
,
(1)
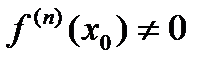 .
.
Воспользуемся для  формулой Тейлора с остаточным членом в форме Пеано:
формулой Тейлора с остаточным членом в форме Пеано:

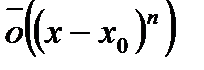 ,
,  ,
,
которая, учитывая условия (1), принимает вид:
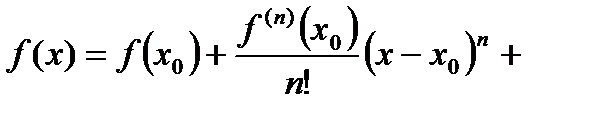
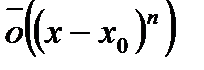 ,
,  . (2)
. (2)
Запишем остаточный член в следующем виде:
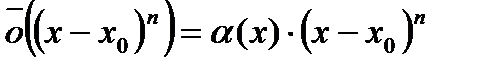 , де
, де 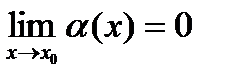 .
.
Тогда из (2) получим:
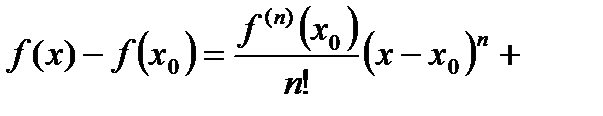
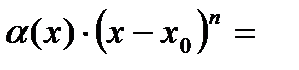
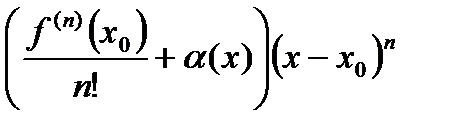 . (3)
. (3)
Поскольку 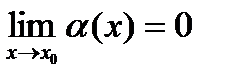 , то для любых
, то для любых 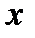 , достаточно близких к
, достаточно близких к 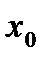 имеем:
имеем:
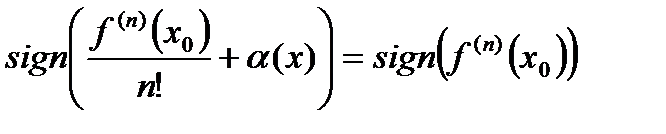 .
.
Рассмотрим два возможных случая для значения 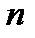 .
.
1. Пусть 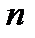 - четное, т.е.
- четное, т.е. 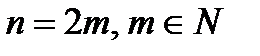 . Допустим, что
. Допустим, что 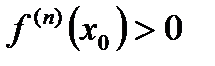 . Тогда при переходе через
. Тогда при переходе через 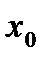 правая часть (3) будет сохранять знак «+», то есть при всех
правая часть (3) будет сохранять знак «+», то есть при всех 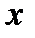 , достаточно близких к
, достаточно близких к 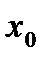 , имеем:
, имеем:
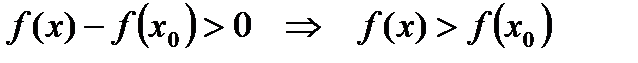 ,
,
т.е. в точке 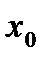 функция имеет локальный минимум.
функция имеет локальный минимум.
Аналогично получим, что когда 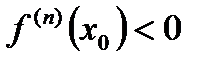 и
и 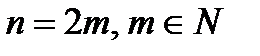 , то
, то  имеет в точке
имеет в точке 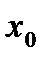 локальный максимум.
локальный максимум.
2. Пусть 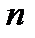 - нечетное, т.е.
- нечетное, т.е.  . Допустим, что
. Допустим, что 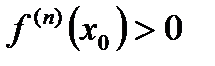 . Тогда для
. Тогда для 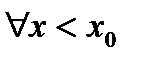 в достаточно малой окрестности
в достаточно малой окрестности 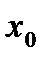 имеем:
имеем:
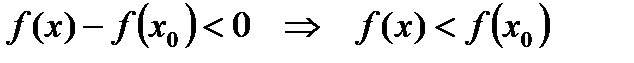 , (4)
, (4)
а для 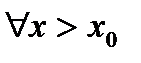 в достаточно малой окрестности
в достаточно малой окрестности 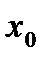 имеем:
имеем:
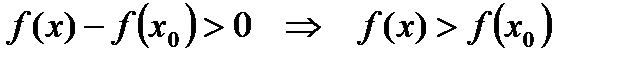 . (5)
. (5)
Из (4) и (5) вытекает, что экстремума в точке 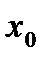 нет.
нет.
Мы доказали следующую теорему.
Теорема 3 (третье достаточное условие локального экстремума). Пусть функция  определена на
определена на 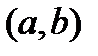 ,
, 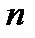 раз дифференцирована в точке
раз дифференцирована в точке 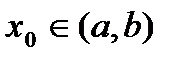 , и выполняются условия (1). Тогда если
, и выполняются условия (1). Тогда если 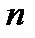 - четное, то
- четное, то  имеет локальный экстремум в точке
имеет локальный экстремум в точке 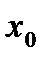 (локальный максимум, когда
(локальный максимум, когда 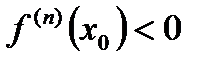 , локальный минимум, когда
, локальный минимум, когда  ). Если
). Если 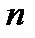 - нечетное, то экстремума в точке
- нечетное, то экстремума в точке 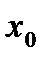 нет.
нет.
Дата добавления: 2015-08-21; просмотров: 1318;
