Теорема Лагранжа. Формула Лагранжа

Теорема (Лагранжа). Пусть функция 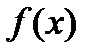определена на 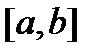и выполняются условия:

1. 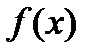непрерывна на ;

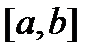2. 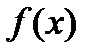дифференцируема в .

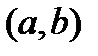Тогда существует точка 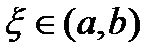, что

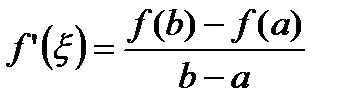. (30)

Доказательство. Построим вспомогательную функцию

.

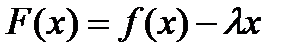Коэффициент 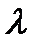выберем так, чтобы выполнялось условие: 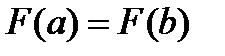. По определению функции 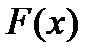это эквивалентно:

,

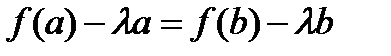откуда

,

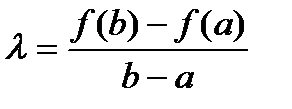а .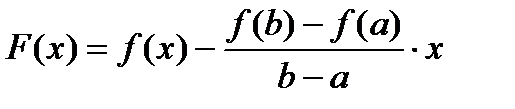

Для 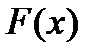выполнены все условия теоремы Ролля, поэтому существует 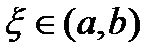, что :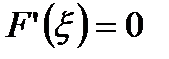

,

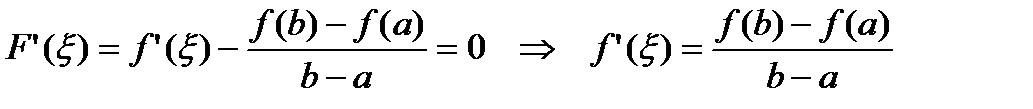что и нужно было доказать.

Формулу (30) можно записать в эквивалентном виде:

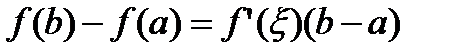. (40)

Формула (40) называется формулой Лагранжа.

Замечание. Теорема Ролля является частным случаем теоремы Лагранжа. Действительно, если к условиям 1,2 теоремы Лагранжа добавить условие 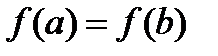, то формула (30) будет иметь вид: 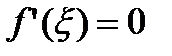, что отвечает теореме Ролля.

Геометрический смысл теоремы Лагранжа понятен из рис.5: если выполняются условия теоремы, то найдется такая точка 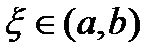, что касательная к графику функция, проведенная в точке , будет параллельна секущей к графику, проведенной через точки , .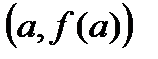

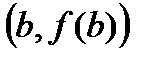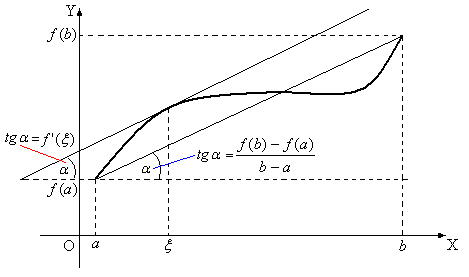
Рис.5.