Состояния машин

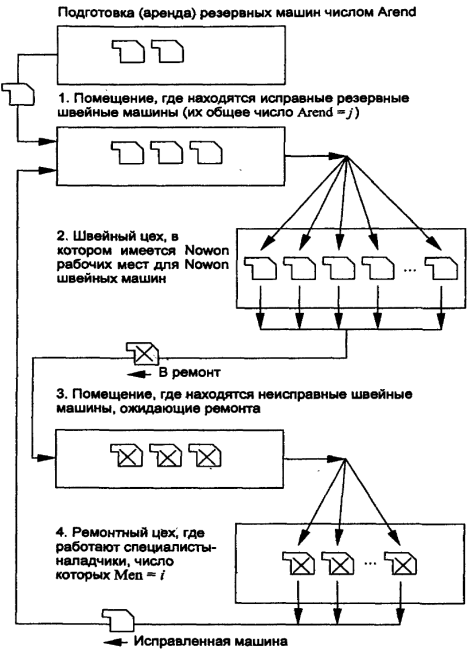
Рис. 8.7. Иллюстрация к задаче оптимизации производственных затрат

В начальный момент решено арендовать Arend машин. Эти машины должны некоторое время находиться в каком-то помещении и «ждать», пока не выйдет из строя машина в цехе. Далее в процессе выхода из строя и восстановления машин в этом помещении будут находиться машины, число которых - случайная величина. Пребывание машин в этом помещении является состоянием 1. Пребывание машин в швейном цехе в исправности - состояние 2.

Если какая-либо машина выходит из строя, то она поступит в ремонт только в том случае, если хотя бы один наладчик свободен (не занят ремонтом другой машины). Вероятность такого события, естественно, не равна единице. Поэтому неисправные машины в ожидании ремонта направляются в другое помещение. Пребывание в этом помещении является состоянием 3. И, наконец, если подходит очередь ремонта неисправной машины, она поступает в ремонтный цех. Ремонт - состояние 4 каждой машины.

Далее начнем строить имитационную модель. Наиболее рациональное решение заключается в том, чтобы выбрать машины в качестве транзактов. В табл. 8.4 приведены типы узлов, имитирующих соответствующие состояния. Количество каналов узла serv в состоянии 2 равно Nowon, а число каналов узла serv в состоянии 4 – это значение Men.

Единственная проблема, с которой мы немедленно столкнемся, заключается в том, что в данной замкнутой схеме нет генераторов транзактов. В связи с этим непонятно, откуда транзакты попадут в модель. Решение этой проблемы довольно простое: необходимо ввести в имитационную модель специальную часть, которая называется схемой зарядки. Рассмотрим эту схему и всю модель на рис. 8.8. Узлы с номерами 1 (queue), 2 (serv), 3 (queue) и 4 (serv) имитируют пребывание машин в состояниях с соответствующими номерами. Эта замкнутая схема не требует дальнейших комментариев.

Далее рассмотрим схему зарядки, которая состоит из трех узлов:

узел 5 (генератор ag), узел 6 (транзактно-управляемый генератор creat) и узел 7 (терминатор term со вспомогательным оператором cheg). Модельное время, в течение которого будем осуществлять эксперимент, задается переменной Protime. Если мы хотим, чтобы это время составляло 3 года, а единицей измерения установим 1 ч, то это время равно 6240,0 ч.

Узел ag генерирует первый транзакт через какой-либо заданный или случайный интервал времени tbeg- Этот интервал можно назвать временем подготовки производства. Сгенерированный первый транзакт (назовем его прародителем) войдет в узел creat. В результате из этого узла выйдут Nowon + Are'nd транзактов, которые поступят в узел 1.

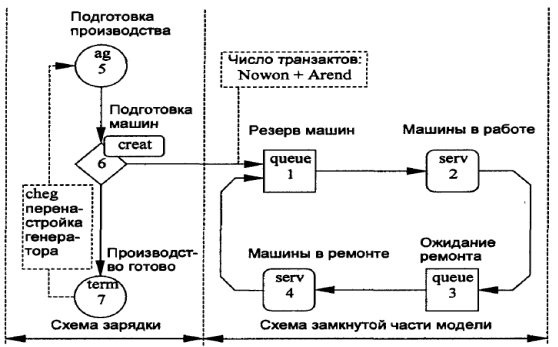
Рис. 8.8. Структурная схема модели для решения задачи минимизации производственных затрат

Первые Nowon транзактов без задержки пройдут этот узел и поступят в узел 2; причем каждый транзакт-машина займет свой канал, т.е. рабочее место. Остальные Arend транзактов останутся в узле 1.

Что касается транзакта-прародителя, то он выйдет из узла creat и войдет в узел term. В этом узле перед уничтожением транзакт- прародитель выполнит операцию cheg для перенастройки генератора ag. Эта операция установит время генерации второго транзакта, равное Protime. Учитывая, что с начала запуска модели уже прошло время t_beg момент генерации второго транзакта будет равен Protime + t_beg (т.е. после выполнения модели). Это означает, что второй транзакт не выйдет из генератора во время моделирования.

Далее перейдем к планированию имитационного эксперимента для определения рационального количества резервных машин и числа специалистов-наладчиков. Возможность существования оптимального решения вытекает из следующих предпосылок.

Нетрудно представить себе, что если число наладчиков мало или равно нулю, то машины в основном будут неисправны, а затраты на производство - велики из-за простоя рабочих мест. Если же число наладчиков очень велико, то будут большими затраты на заработную плату (рис. 8.9,а). Но при отсутствии наладчиков машины постепенно выйдут из строя, а затраты из-за простоя рабочих мест будут велики.

Что касается резервных машин, то, если их число мало или равно нулю, затраты на производство будут велики из-за простоя рабочих мест. Если же число арендуемых машин очень велико, то будут большими затраты на их аренду (рис. 8.9,6).

Поэтому можно допустить гипотезу о наличии какой-то поверхности оптимизации затрат (8.9,в). Однако, учитывая, что число наладчиков и количество машин - целые величины, эта поверхность включает в себя только точки с целочисленными координатами Men и Arend.

Необходимо найти минимальное значение на поверхности затрат E_ij и соответственно значения координат i_opt (переменная Men) и j_opt (переменная Arend). Не будем применять сложные методы поиска экстремальных значений на поверхности оптимизации затрат. Задача решается методом перебора, так как число возможных вариантов, которые необходимо сравнить, невелико. Однако в более сложных случаях требуется применять регрессионный анализ и строить поверхность отклика 2-го порядка.

Первое, что нужно сделать при проведении имитационного эксперимента, - это привести все времена и темпы затрат к одним единицам измерения. С помощью табл. 8.3 получим табл. 8.5 со статьями ежедневных расходов на производство. В ней три строки. Обозначим значение, указанное в каждой строке, как A_k , k = 1,2,3.

Таблица 8.5

Статьи ежедневных расходов А_k, (k= 1,2,3)

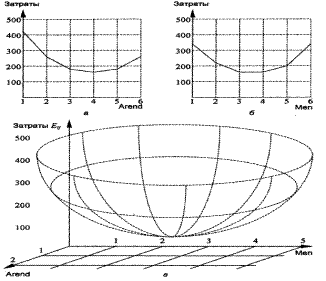
Рис. 8.9. Ингерпретация возможности минимизации затрат:

а - зависимость затрат от числа арендуемых машин Arend при фикс1фованном числе наладчиков; б - зависимость затрат от числа наладчиков Men при фиксированном числе арендуемых машин; в — предполагаемая поверхность оптимизации

Далее потребуется имитационная модель, схема которой была приведена на рис. 8.8. С ее помощью необходимо получить значения загрузки рабочих мест, например, с экрана (рис. 8.10).

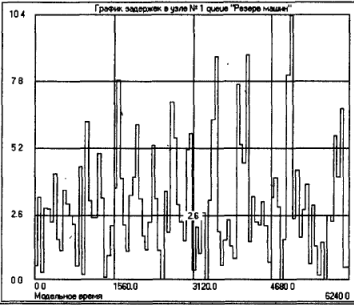
Рис8.10. Окно с результатами моделирования

Построим матрицу загрузок для различных значений числа наладчиков i и количества швейных машин j . Элементы такой матрицы обозначим B_ij. Пример матрицы представлен в виде табл. 8.6. Как было показано выше, в оценочном и не совсем верном расчете, поиск оптимальных значений i и j можно начать со значений i = 3 и j = 3, пропустив меньшие значения (i - число наладчиков, i = 3,4, 5; j - число арендуемых швейных машин, j = 3,4, 5).

Таблица 8.6

Загрузка рабочих мест Вij

(получается с помощью имитационной модели)

Далее определим ежедневные затраты на оплату труда наладчиков и аренду резервных машин. Для этого создадим еще одну матрицу (табл. 8.7) элементов C_ij с той же размерностью, какая существует в табл. 8.6. Элементы этой матрица определяются с помощью табл. 8.5 из соотношения

Cij=A₁i + A₂j, i = 3,4, 5, j = 3,4, 5.

Таблица 8.7

Затраты на оплату труда наладчиков и аренду резервных машин Q

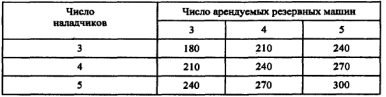
Перейдем к определению потерь из-за снижения объемов производства по причине простоя рабочих мест. Для этого построим матрицу (табл. 8.8) элементов Dij с той же размерностью. Элементы этой матрицы определяются с помощью табл. 8.5 и 8.6. Элементы B_ij табл. 8.6 - это загрузка оборудования р при конкретных значениях i и j. Поэтому справедливо следующее соотношение:

D_ij= Nowon(1-В_ij)А₃, i = 3,4,5, j = 3,4,5.

Таблица 8.8