Диаграммы плавкости бинарных систем с образованием химического соединения, плавящегося конгруэнтно

Диаграммы состояния такого типа характерны для систем, в которых исходные компоненты А и В образуют одно прочное химическое соединение А_mB_n, плавящееся без разложения (конгруэнтно) и не растворимое в компонентах А и В в твердом состоянии.

Во многих случаях кривая ликвидуса двухкомпонентных систем, в отличие от диаграмм 10.4 – 10.6, имеет один (рис. 10.7) или даже несколько максимумов. Поскольку температура затвердевания любого вещества понижается при добавлении к нему других компонентов, то форму таких кривых можно объяснить лишь тем, что в точке максимума образуется химическое соединение. Температура плавления такого соединения понижается при добавлении к нему как компонента А, так и компонента В. Если образовавшееся химическое соединение А_mB_n устойчиво как твердом, так и в жидком состояниях (например, для систем H₂O и FeCl₃, уксусная кислота и мочевина), т. е. обладает определенной температурой плавления, то точку максимума называют конгруэнтной. Иными словами, плавление химических соединений, при котором состав твёрдой фазы одинаков с составом расплава, называется конгруэнтным. Примерами систем с одним конгруэнтно плавящимся соединением являются Sn – Mg, Mg – Si и CaCl₂ – KCl.

Конгруэнтной точкой на диаграмме 10.7 является фигуративная точка с. В ней система условно инвариантна

.

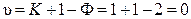Фигуративные точки, лежащие на линии cd, соответствуют твердому химическому соединению при различных температурах:

.

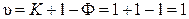В различных системах вид максимума на кривой ликвидуса разный и зависит от степени диссоциации соединения при температуре плавления по схеме

А_mB_n « mA + nB.

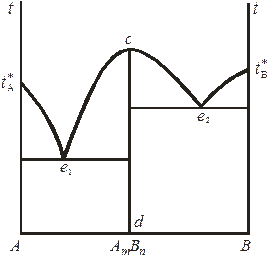
Рис. 10.7. Диаграмма плавкости бинарной системы

с конгруэнтной точкой плавления

Чем больше степень диссоциации химического соединения, тем более пологим будет максимум на кривой ликвидуса (соответственно, чем меньше степень диссоциации, тем острее максимум). Радиус кривизны максимума r и степень диссоциации химического соединения α связаны между собой следующим приближенным соотношением:

,

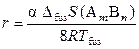где Δ_fusS (А_mB_n) и T_fus – энтропия и температура плавления соединения.

Результатом частичной диссоциации химического соединения (см. рис. 10.7) является то, что в расплаве левее линии сd присутствуют некоторые количества компонента В, а правее – некоторые количества компонента А.

Если степень диссоциации химического соединения равна нулю, то на кривой ликвидуса наблюдается острый максимум. Фигуративная точка с, отвечающая недиссоциированному химическому соединению, называется сингулярной или дальтоновской точкой, а само соединение – дальтонидом. Характерным признаком образования дальтонидов является то, что их состав не зависит от внешних условий, определяющих равновесие (температура или давление). Примерами систем с образованием дальтонидов являются Mg – Ag, Mg – Au, Au – Zn.

Если на кривой ликвидуса имеется пологий максимум, не соответствующий простому стехиометрическому соотношению исходных компонентов и смещающийся при изменении внешних параметров (например, давления), то твердое соединение в таких системах называется бертоллидом. Бертоллиды – твердые фазы переменного состава, стоящие на границе между химическими соединениями и твердыми растворами. Примерами систем с образованием бертоллидов являются Pb – Na, Al – Fe и Fe – Sb.

Итак, если соединение А_mB_n имеет определенную точку плавления и ведет себя как индивидуальное химическое соединение, то общая диаграмма состояния (см. рис. 10.7) как бы разделяется на две диаграммы: первая диаграмма – левее линии сd, относящаяся к системе А и А_mB_n (эвтектическая точка e₁); вторая диаграмма – правее линии сd, относящаяся к системе В и А_mB_n (эвтектическая точка e₂).

Если исходные компоненты А и В образуют несколько химических соединений, плавящихся конгруэнтно, на диаграмме плавкости каждому из них соответствует свой максимум. Примерами таких систем являются Ag – Ca, Cu – Mg и Al₂O₃ – CaO.