Дифференциальные уравнения гидростатики (равновесия). Закон Паскаля

Для выяснения закона распределения гидростатического давления в покоящейся жидкости рассмотрим общий случай равновесия жидкого тела, находящегося в состоянии относительного покоя.

Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед (рис. 3.3) со сторонами 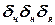и центром в точке Ц. Рассматриваемый параллелепипед находится в покое под действием: а) поверхностных сил давления окружающей жидкости, направленных внутрь параллелепипеда нормально к его граням; б) объемных (массовых) сил, действующих на каждую частицу жидкости (силы тяжести и силы инерции переносного движения в случае относительного покоя).

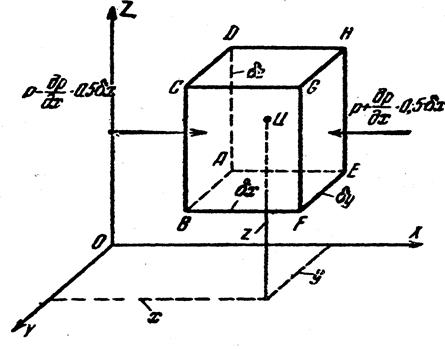
Рис. 3.3

Пусть р — гидростатическое давление в точке Ц.

Тогда, учитывая непрерывность изменения напряжения в жидкой среде и пренебрегая величинами бесконечно малыми, стремящимися к нулю при уменьшении параллелепипеда до размеров точки, мы можем определить среднее гидростатическое напряжение на соответствующих гранях параллелепипеда по следующим выражениям:

для грани ABCD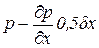

для грани EFGH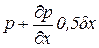

Аналогичные выражения могут быть написаны и для гидростатических напряжений по другим граням.

Равнодействующую массовых сил, действующих на единицу массы жидкости (ускорение массовых сил), обозначим через F, а проекции ее на оси координат — соответственно через F_x, F_y, F_z и на любое направление — через F_n..

Тогда, условие равновесия сил, действующих на выделенный параллелепипед, заключающееся в равенстве нулю суммы проекций всех сил на избранное направление, можно записать, например, для оси ОХ в виде

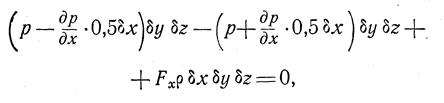
Или

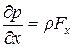
Вообще, очевидно, для любого избранного направления будем иметь:

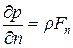
Система уравнений

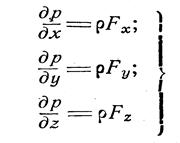
представляет собой общие условия равновесия жидкости, данные Эйлером.

Умножив уравнения Эйлера соответственно иа dx, dy, dz и сложив их, получим:

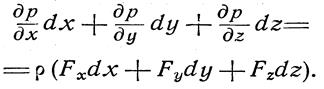
Учитывая, что левая часть уравнения представляет собой полный дифференциал гидростатического давления, получим:

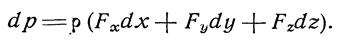
Уравнение (14) может иметь смысл только при условии, что и выражение в скобках в правой части его также представляет собой полный дифференциал некоторой функции U(x у, z), которую по аналогии с теоретической механикой назовем силовой функцией. Следовательно, проекции ускорения массовых сил должны определяться следующими соотношениями:

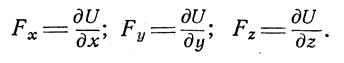
Как известно из теоретической механики, в этом случае должна существовать некоторая функция координат П(х, у, х), называемая потенциальной энергией, равная силовой функции, взятой с обратным знаком. Из этого следует:

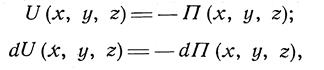
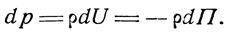
Интегрируя (15), получим

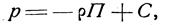
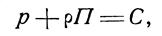
где С — произвольная постоянная интегрирования.

В нашем случае потенциальная энергия относится к единице массы, и поэтому будем ее называть удельной потенциальной энергией.

В формуле (16) удельная потенциальная энергия П и давление р соответствуют одной и той же частичке жидкости, находящейся в относительном покое.

Для двух частиц одного и того же объема одной и той же однородной жидкости уравнение (16) можно написать в виде

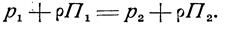
Поверхностью равного давления в жидкости называется поверхность, все точки которой испытывают одинаковое давление.

Уравнение такой поверхности мы получим из (14) или (17), полагая р = const или: dp = 0. При этом

F_xdx + F_ydy + F_zdz = 0, (18)

или

П(х, у, z) = const. (19)

Таким образом, все частички жидкости, расположенные на поверхности равного давления, обладают одинаковой удельной потенциальной энергией, соответствующей массовым силам.

Одной из поверхностей равного давления является свободная поверхность жидкости, т. е. поверхность жидкости, граничащая с газовой средой (в гидротехнике обычно с воздухом), так как во всех ее точках давление равно внешнему давлению р₀.

Уравнение поверхности равного давления (18) можно рассматривать как уравнение работы массовых сил при элементарном перемещении по поверхности равного давления. Из равенства нулю этой работы следует:

ускорение массовых сил, действующих на жидкость, находящуюся в относительном покое, в любой точке жидкости направлено по нормали к поверхности равного давления, проходящей через эту точку.

В условиях земного притяжения в гидростатике из массовых сил действует только сила тяжести. Принимая положительным направление оси z вертикально вверхисчитая для небольших поверхностей силы тяжести параллельными друг другу, будем иметь:

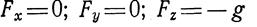
исогласно (14)

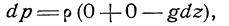
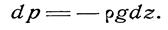
Интегрируя (20), получим:

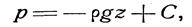
или (так как pg = )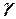

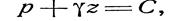
где С — произвольная постоянная интегрирования.

Полученное уравнение делением обеих частей на 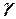можно привести к виду

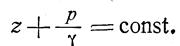
Для любых двух частиц одного и того же объема жидкости уравнение (21) можно представить в виде

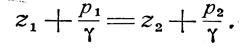
Это уравнение выражает гидростатический закон распределения давления и называется основным уравнением гидростатики.

Основное уравнение гидростатики было получено ранее при помощи анализа действия сил, поделив формулу (10) на 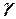мы получим правую часть формулы (21). Однако зависимость, полученная интегрированием дифференциальных уравнений движения, имеет более обобщенный характер.

Основное уравнение гидростатики (22) может быть использовано для обоснования закона Паскаля.

Возьмем внутри однородной покоящейся жидкости две произвольные точки с отметками z₁ и z₂ относительно некоторой произвольно выбранной плоскости отсчета. Давления в этих точках равны соответственно р₁ и р₂ и связаны уравнением (22).

Увеличим, не нарушая равновесия, в точке z₁ давление на 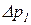. В этом случае соответственно должно измениться давление и в точке z₂ на величину 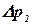. Для нового состояния основное уравнение будет иметь вид

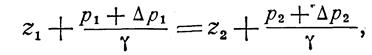
что дает:

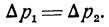
Отсюда следует так называемый закон Паскаля:

всякое изменение давления в какой-либо точке покоящейся жидкости, не нарушающее ее равновесия, передается в остальные ее точки без изменений.

Для решения прикладных задач важно уметь определять гидростатическое давление в точке.

Пусть z — координата произвольной точки А (рис. 3.4) внутри покоящейся жидкости, в которой необходимо определить давление р. z ₀— координата точки В того же объема, давление в которой известно и равно р₀

Применим основное уравнение гидростатики (22):

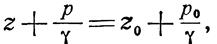
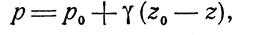
где 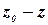есть не что иное, как глубина погружения одной точки под другой.

Из этой формулы следует, что чем ниже расположена точка, тем большее давление она испытывает.

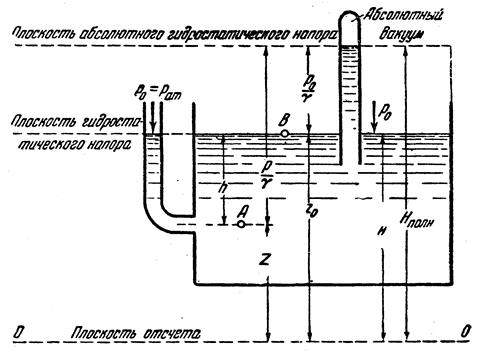
Рис.3.4. Схема для определения гидростатического давления в точке

Если точка В взята на свободной поверхности (рис. 3.4), то z₀—z есть глубина h погружения точки, а 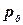— давление на свободной поверхности и

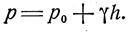
Формула (24) является формулой гидростатического давления в точке на глубине h под свободной поверхностью.

Таким образом, гидростатическое давление в данной точке покоящейся жидкости складывается из внешнего давления на поверхности 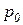и давления 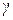h, зависящего только от глубины погружения h и удельного веса жидкости .

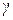В гидротехнической практике в большинстве случаев внешним давлением является давление атмосферы ( ).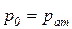

Эпюра гидростатического давления на наклонную стенку показана на рис. 3.5, а давление в точке поверхности находится по формуле

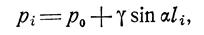
т.е. в системе координат р, l зависимость 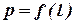изображается прямой линией. Треугольник АВС представляет собой диаграмму давления и называется эпюрой манометрического давления.

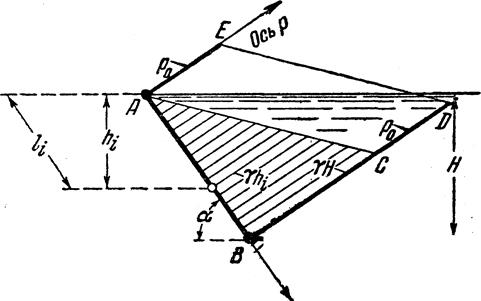
Рис.3.5. Схема к определению гидростатического давления на стенку

Заметим, что стеклянная трубка может служить для измерения давления в жидкости и поэтому называется пьезометром