Гидростатическое давление и его свойства

Массовыми силами являются силы, пропорциональные массе жидкости: силы тяжести и инерционные силы.

Жидкость, помещенная в резервуар, оказывает давление, как на его стенки, так и на дно, зависящее от плотности жидкости и места положения рассматриваемой точки. Так, вода и ртуть при одинаковых прочих условиях будут оказывать разное силовое воздействие на стенки сосуда, а частицы жидкости, находящиеся внизу, будут сжиматься сильнее, чем верхние.

Гидростатическое давление и его свойства

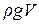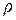Рассмотрим резервуар, представленный на рис.3.1а. На дно резервуара площадью abсd оказывает воздействие вес налитой жидкости, т. е. Р= , где — плотность жидкости; V — ее объем. Воздействие силы Р на площадь дна 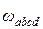представляет среднее гидростатическое давление .

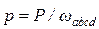Выделим на боковой поверхности небольшую площадку , силу давления на нее обозначим через 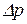. Отношение будет также средним гидростатическим давлением в пределах выделенной площадки. Если теперь выделенную площадку уменьшать до нуля, то 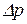будет также стремиться к нулю, а отношение в пределе будет представлять собой гидростатическое давление (обозначается буквой р) в точке:

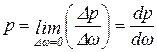(1)

В качестве единицы этой величины применяют Па. Под паскалем понимают давление, создаваемое силой в 1н, равномерно распределенной по нормали к поверхности площадью 1 м².

Итак, гидростатическое давление в точке является пределом отношения силы гидростатического давления, действующей на элементарную площадку к самой элементарной площадке, если последняя стремится к точке.

Рассмотрим свойства гидростатического давления. На вертикальной левой стенке резервуара (рис. 3.1, а) выделим элементарную площадку 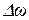. Предположим, что реакция стенки на жидкость будет приложена в точке А и направлена к ней под углом φ. Вектор R можно разложить на два направления — нормальное к стенке и касательное вдоль стенки: R_n и . Сила R_n вызывает в жидкости сжатие, чему жидкость легко противостоит. Сила должна была вызвать перемещение частиц жидкости вдоль стенки, но этого мы не наблюдаем (все рассматривается для случая покоя жидкости). Наше предположение о том, что вектор R направлен под углом — неверно.

Рис.3.1.

Отсюда следует:

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Выделим из жидкости, заполняющей объем резервуара (рис. 3.1, а), элементарный кубик со сторонами dх, dy, dz (рис. 3.1,б). Так как кубик находится в равновесии, то это значит, что уравновешены поверхностные и массовые силы по всем трем осям:

, (2)

, (3)

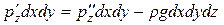(4)

где dxdydz — объем кубика.

Сократив равенства, получим

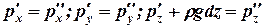(5)

Членом pgdz, бесконечно малым по сравнению с 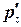^r и 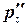можно пренебречь, т. е.

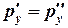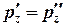; ; (6)

Так как кубик не деформируется (не вытягивается вдоль одной из осей, жидкость находится в покое), давления по различным осям одинаковы, а именно

= = (7)

Итак, приходим к выводу:

Свойство 2. Гидростатическое давление неизменно во всех направлениях гидростатическое давление в любой точке одинаково по всем направлениям.

Рис 3.2.

Третьим свойством гидростатического давления является зависимость его от координат пространства p=f(x, y, z).

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Выясним характер этой зависимости. Выделим из жидкости, заполняющей резервуар (рис. 3.2), параллелепипед с основанием 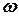и высотой h. Давление на свободной поверхности резервуара равно p_0. Поскольку параллелепипед внутри жидкости находится в равновесии, то , . Сила, действующая с торца параллелепипеда , уравновешивается силой давления р₀ и силой веса жидкости в объеме параллелепипеда, т. е.

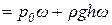(9)

Разделив полученное равенство на 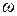, получим:

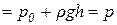/ω (10)

где р — гидростатическое давление жидкости на глубине h.

Это уравнение является основным уравнением гидростатики.

Полученное уравнение означает: полное или абсолютное давление в любой точке покоящейся жидкости слагается из давления на ее свободной поверхности р₀ и давления 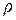gh, созданного весом выше лежащего слоя жидкости (так называемого столба жидкости).

В открытом резервуаре, находящемся на поверхности земли, первое слагаемое в последнем уравнении равно атмосферному давлению, второе слагаемое 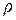gh называется избыточным давлением:

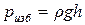(12)

В водоеме на глубине 10 м согласно (12)

= 1000 кг/м³ ×9,8 м/с² × 10 м=98 000 Па.

Таким образом, давление 1 м столба жидкости равно 9,8 кПа.