Лекция.
Таќырыбы: Жазықтықтағы түзудің берілу тәсілдері.Екі түзу арасындағы бұрыш. Түзулердің параллельдік және перпендикулярлық шарты.
Жазықтықтағы түзудің берілу тәсілдері.
Жазықтықта кез-келген түзу берілсін және ол Х осімен 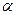 градус бұрыш жасасын.Онда ол бұрыштық tg
градус бұрыш жасасын.Онда ол бұрыштық tg 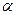
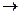 бұрыштық коэффицент деп аталады және k әрпімен белгіленеді.Түзу бойында жатқан
бұрыштық коэффицент деп аталады және k әрпімен белгіленеді.Түзу бойында жатқан 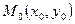 және
және 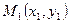 нүктелері берілсін.
нүктелері берілсін. 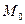 нүктесінен
нүктесінен 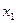 осіне
осіне 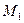 нүктесінен у осіне параллель жүргізейік.Қиылысу нүктесін В әріпімен белгілейік.
нүктесінен у осіне параллель жүргізейік.Қиылысу нүктесін В әріпімен белгілейік.
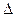
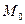 В
В 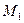
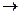 tg
tg 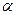
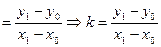 /1/
/1/
Түзудің бұрыштық коэффиценті k мен у осінен қиып өтетін В шамасы берілсін.Түзу бойынан кез-келген М нүктесін алайық (түзу теңдеуін сипаттау үшін).Түзуменен у осінен қиылысу нүктесінен х осіне 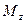 нүктесінен у осіне параллель жүргізейік.Сонда
нүктесінен у осіне параллель жүргізейік.Сонда 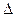 SM
SM 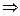
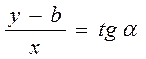
 /2/
/2/
/2/ бұрыштық коэффицент арқылы берілген түзудің теңдеуі.
Түзудің бұрыштық коэффиценті k мен түзудің бойында жататын 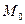 нүктесі берілсін.Түзу бойынан кез-келген М нүктесін алайық.
нүктесі берілсін.Түзу бойынан кез-келген М нүктесін алайық. 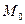 нүктесінен х осіне М нүктесінен у осіне параллель жүргізейік.
нүктесінен х осіне М нүктесінен у осіне параллель жүргізейік.
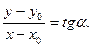
 /3/
/3/
/3/ Бұрыштық коэффиценті k. Болатын және 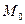 нүктесі арқы лы өтетін түзудің теңдеуі. Түзу бойында жатқан
нүктесі арқы лы өтетін түзудің теңдеуі. Түзу бойында жатқан 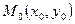 және
және 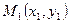 нүктесі берілсін. Онда /1/ формула бойынша
нүктесі берілсін. Онда /1/ формула бойынша
/1/ 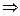
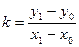
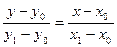 /4/
/4/
/4/ екі нүкте арқылы өтетін түзудің теңдеуі.
Анықтама: 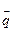 векторы түзудің бағыттауыш векторы деп аталады егер түзуде жатқан кез-келген векторға коллинеар болса.
векторы түзудің бағыттауыш векторы деп аталады егер түзуде жатқан кез-келген векторға коллинеар болса.
Түзудің 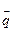 бағыттауыш векторымен түзу бойында жатқан
бағыттауыш векторымен түзу бойында жатқан 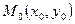 нүктесі берілсін.
нүктесі берілсін.
Түзу бойынан кез-келген М нүктесін алайық.(түзу теңдеуін сипаттау үшін). Онда 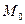 М =
М = 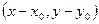 .
. 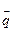 =(l, m)
=(l, m) 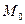 векторымен
векторымен 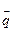 векторларыколлинеар.Екі вектордың коллинеарлық шартын пайдалансақ,
векторларыколлинеар.Екі вектордың коллинеарлық шартын пайдалансақ, 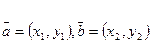
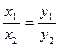 ;
; 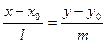 /5/
/5/
/5/ түзудің канондық теңдеуі.
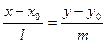 =t
=t

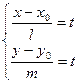
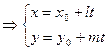 /6/
/6/
/6/ түзудің параметрлік теңдеуі.
Анықтама: 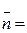 (АВ) векторы түзудің нормалы деп аталады,егер түзудегі кез-келген векторға артоганаль болса.
(АВ) векторы түзудің нормалы деп аталады,егер түзудегі кез-келген векторға артоганаль болса.
Түзудің 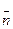 мен түзу бойында жатқан кез-келген
мен түзу бойында жатқан кез-келген 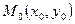 нүктесі берілсін.Түзу бойынан М нүктесін алайық (түзу теңдеуін сипаттау үшін).Онда
нүктесі берілсін.Түзу бойынан М нүктесін алайық (түзу теңдеуін сипаттау үшін).Онда 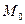 М=
М= 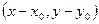
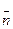 =(АВ) векторлары артоганаль.Екі артоганальдың перпендикулярлық шартын пайдаланайық:
=(АВ) векторлары артоганаль.Екі артоганальдың перпендикулярлық шартын пайдаланайық:
А(х- 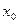 )+В(у-
)+В(у- 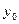 )=0 /7/
)=0 /7/
/7/ 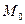 нүктесі арқылы өтетін және М нормалы бар теңдеуі.
нүктесі арқылы өтетін және М нормалы бар теңдеуі.
Ах+Ву+(А 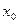 -В
-В 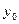 )=0
)=0
С=-(А 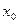 -В
-В 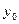 )
)
Ах+Ву+С=0 /8/
/8/ түзудің жалпы теңдеуі.
С 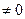 Ах+Ву =-С
Ах+Ву =-С
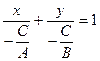
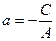
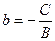
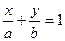 /9/
/9/
/9/ түзудің кесіндідегі теңдеуі
Түзудің кесіндідегі теңдеуін келесі геометриялық мағынасы бар,яғни Х осінен а-ға тең шамалы У осінен в-ға тең шаманы алып,оларды қоссақ, онда ізденілген түзудің кескіні шығады.
1)С=0 Ах+Ву=0 О(0;0)
Егер С=0 болса,онда түзу координаталар басынан өтеді О(0;0)
2)А=0 В  С
С 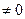 у=-
у=- 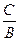
Онда түзу у=- 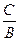 арқылы өтеді және ОХ осіне параллель.
арқылы өтеді және ОХ осіне параллель.
3)В=0 А 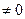 С
С 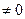 Х
Х 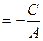
Түзу 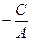 нүктесі арқылы өтеді және ОУ осіне параллель.
нүктесі арқылы өтеді және ОУ осіне параллель.
4)А=С=0 В 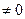 у=0
у=0
Түзу ОУ осімен беттеседі.
5) В=С=0 А 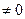 х=0
х=0
Түзу ОХ осімен беттеседі.
А және В сандары бір мезгілде екеуі де 0-ге тең болмайды.
Екі жазықтықтың арасындағы бұрыш
1)Бұрыштық коэфиценті арқылы берілген бұрыш.
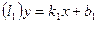
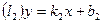 екі түзудің бұрыштық коэффициенті арқылы берілсін.
екі түзудің бұрыштық коэффициенті арқылы берілсін. 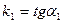
 екі түзу арасындағы
екі түзу арасындағы 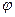 бұрышын табайық.
бұрышын табайық.
Х осіне параллель түзу жүргізейік.
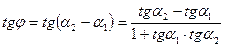
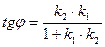 /1/
/1/
/1/ бұрыштық коэффициенті арқылы берілген бұрыштың теңдеуі
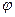 =0
=0 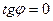
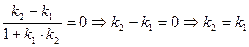 /2/
/2/
/2/
2)Жалпы теңдеу арқылы
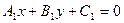

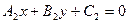

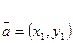
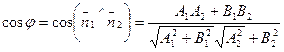
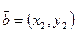
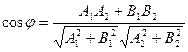 /3/
/3/
/3/ жалпы теңдеу арқылы берілген түзу арасындағы бұрыш теңдеуі.
Екі түзу параллель болса, онда лоардың нормалдары коллинеар
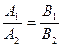 /4/
/4/
/4/ екі түзудің параллельдік шарты.
Екі түзу перпендикуляр болса,онда олардың нормалдары ортоганаль болады.
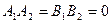 /5/
/5/
/5/ жалпы теңдеу арқылы беріл-
ген 2 түзудің перпендикуляр-
лық шарты.
3)Канондық теңдеу арқылы берілген түзу теңдеуі
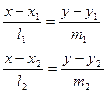
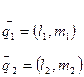
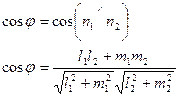 /6/
/6/
/6/ канондық теңдеуі арқылы берілген түзулер арсындағы бұрышты анықтау формуласы.
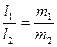 /7/
/7/
/7/ параллельдік шарты.
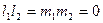 /8/
/8/
/8/ перпендикулярлық шарты.
Дата добавления: 2015-08-20; просмотров: 4398;
