Лекция. Таќырыбы: Екі,үш,төрт вектордың сызықтық комбинациясы
Таќырыбы: Екі,үш,төрт вектордың сызықтық комбинациясы. Аффиндік координаталар. Базалар.
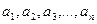 векторларының сызықтық тәуелділігі деп осы вектордың кез келген нақты сандарға көбейтілген қосындылары айтамыз:
векторларының сызықтық тәуелділігі деп осы вектордың кез келген нақты сандарға көбейтілген қосындылары айтамыз: 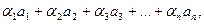
мұндағы 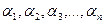 - кез келген нақты сандар.
- кез келген нақты сандар.
1-анықтама. Егер 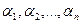 нақты сандарының ішінде нөлге тең болмайтын бір сан болса, онда
нақты сандарының ішінде нөлге тең болмайтын бір сан болса, онда 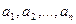 векторларының осы сандарға көбейтінділерінің қосындысы сызықтық тәуелді векторлар деп аталады, яғни мынадай теңдік орындалады.
векторларының осы сандарға көбейтінділерінің қосындысы сызықтық тәуелді векторлар деп аталады, яғни мынадай теңдік орындалады. 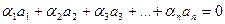
2-анықтама.Егер 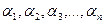 сандарының бәрі де нөлге тең болса онда
сандарының бәрі де нөлге тең болса онда 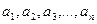 векторлары тәуелді емес сызықтық векторлары деп аталады.
векторлары тәуелді емес сызықтық векторлары деп аталады.
3-анықтама. Егер векторлар бір жазықтықтың бойында немесе параллель жазықтықтардың бойында жатса, онда олар компланарлық векторлар деп аталады.
1-теорема. Екі вектордың сызықтық тәуелді болуы үшін олардың коллинеар болу қажетті және жеткілікті.
Д ә л е л д е м е . a, bвекторларының өз ара сызықтық байланысы болсын. Жоғарыда айтылған сызықтық тәуелділіктің бірінші анықтамасы бойынша 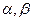 сандарының біреуі нөлге тең болмаса , онда мына
сандарының біреуі нөлге тең болмаса , онда мына 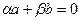 теңдігі орындалуы керек. Олай болса
теңдігі орындалуы керек. Олай болса 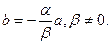 Егер
Егер 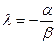 деп белгілесек , онда
деп белгілесек , онда 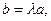 яғни қажетті шарты осы болады.
яғни қажетті шарты осы болады.
Енді aжәнеbвекторлары өз ара коллинеар болсын. Бұл векторлардың сызықтық тәуелділігін көрсетейік. Коллинеарлық векторлар - өз ара сызықтық тәуелді болатын векторлар. Өйткені aжәнеbвекторларының біреуі нөлге тең болса ,онда aжәнеbвекторларының сызықтық байланысы да нөлге тең болады.Егер aжәнеbвекторларының екеуі де нөлге тең болмайтын векторлар болса, онда екі вектордың коллинеарлық шарты бойынша 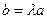 немесе
немесе 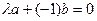 болады. Мұндағы
болады. Мұндағы 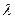 және -1 сандарының біреуінің нөлден өзгеше екендігі айқын. Ендеше
және -1 сандарының біреуінің нөлден өзгеше екендігі айқын. Ендеше 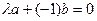 , бұл теңдік екі вектордың тәуелділігін көрсетеді. Екі вектордың сызықтық байланысының жеткілікті шарты осы болады.
, бұл теңдік екі вектордың тәуелділігін көрсетеді. Екі вектордың сызықтық байланысының жеткілікті шарты осы болады.
2-теорема. Үш вектордың сызықтық тәуелді болуы үшін олардың компланар болу қажетті және жеткілікті.
Д ә л е л д е м е . а) Қажетті шарт. a, b, c векторларының өз ара сызықтық тәуелділігі болсын. Олардын компланар екенін дәлелдейік. Сызықтық байланыстың анықтамасы бойынша мынадай  нақты үш сандар табылады. Бұлардың біреуі нөлге тең болмаса, онда
нақты үш сандар табылады. Бұлардың біреуі нөлге тең болмаса, онда 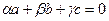 теңдігі орындалуға тиіс. Мысалы,
теңдігі орындалуға тиіс. Мысалы, 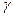 нөлге тең болмаса, онда
нөлге тең болмаса, онда 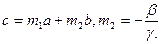 . Егер a, b, c векторларының бастапқы нүктелері бас нүктеден (0) жүргізілсе, онда с параллелограмының
. Егер a, b, c векторларының бастапқы нүктелері бас нүктеден (0) жүргізілсе, онда с параллелограмының 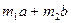 теңдігін алайық. Бұдан
теңдігін алайық. Бұдан 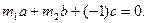
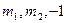 сандарының біреуі нөлден өзгеше
сандарының біреуі нөлден өзгеше
болғандықтан , бұл соңғы теңдік үш вектордың сызықтық тәуелділігін көрсетеді. Бір О нүктесін алып үш векторды бір жазықтықтың бойына орналастырсақ, онда
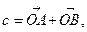
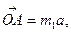 мұндағы
мұндағы 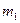 - нақты сан,
- нақты сан,
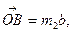 мұндағы
мұндағы 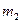 - нақты сан,
- нақты сан,
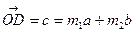 немесе
немесе 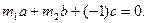 ,мұндағы
,мұндағы 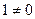 нөлге тең емес.
нөлге тең емес.
Енді төрт вектордың сызықтық байланыстарын қарастырайық.
3-теорема. Кез келген төрт вектор сызықтық тәуелді.
a, b, c, R векторларының сызықтық байланыстарын қарастыру үшін бұларды бір 0 нүктесінен бастап салып, осыларға сәйкес парллелепипед құрсақ (138-сызба), онда мынадай теңдік шығады:
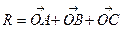 .
.
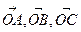 векторлары нөл болмайтын a, b,c векторларына коллинеар болғандықтан, олардың әрқайсысына сәйкес
векторлары нөл болмайтын a, b,c векторларына коллинеар болғандықтан, олардың әрқайсысына сәйкес 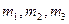 нақты сандар болады. Ендеше, мына теңдік орындалады.
нақты сандар болады. Ендеше, мына теңдік орындалады.
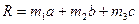
яғни
. 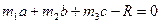
Бүл төрт вектордың компланар болмайтын және өз ара сызықтық тәуелділігін көрсететін теңдік. Қорыта келгенде мына негізгі үш формуланың мағынасын жақсы ұғыну керек:
1) 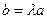 ,
,
2) 
3) 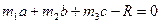 .
.
Бірінші формула бір түзудің бойындағы екі вектордың сызықтық байланысын және бұл екі вектордың коллинеарлық шартын көрсетеді. Екінші формула бір жазықтықтың бойындағы үш вектордың сызықтық байланысын және олардың компланар екендігін көрсетеді. Үшінші формула компланар емес 4 вектордың байланысын көрсетеді.
Базис және аффиндік координаталар.
Әуелі базис, сонан кейін аффиндік координаталар туралы ұғым берейік.
1-анықтама. a, b,c векторларының өз ара сызықтық тәуелділігі болмай, олар кез келген нақты 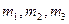 сандары арқылы бір R векторымен сызықтық байланыста болса, онда a, b,c векторлары бір базис жасайды дейміз. Басқаша айтқанда, R векторы
сандары арқылы бір R векторымен сызықтық байланыста болса, онда a, b,c векторлары бір базис жасайды дейміз. Басқаша айтқанда, R векторы 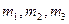 сандары арқылы a, b,c векторларына жіктеледі:
сандары арқылы a, b,c векторларына жіктеледі: 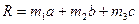 Мұны былай деуге болады: кез келген компланар емес үш a, b, cвекторы кеңістікте бір базис жасайды. Онда жоғарыда айтылған базистің анықтамасы бойынша кез келген Rвекторына сәйкес
Мұны былай деуге болады: кез келген компланар емес үш a, b, cвекторы кеңістікте бір базис жасайды. Онда жоғарыда айтылған базистің анықтамасы бойынша кез келген Rвекторына сәйкес 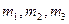 нақты сандары табылып, мына
нақты сандары табылып, мына 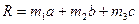 теңдігі орындалады. Бұл теңдікR векторының a, b, cбазисіне жіктелуі деп аталады, ал
теңдігі орындалады. Бұл теңдікR векторының a, b, cбазисіне жіктелуі деп аталады, ал 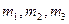 сандары Rвекторының a, b, cбазисіне қарағандағы координаталары деп аталады.
сандары Rвекторының a, b, cбазисіне қарағандағы координаталары деп аталады.
2-анықтама. Егер кез келген жазықтықтағы с векторына нақты 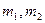 сандары табылып, мына
сандары табылып, мына  теңдігі орындалса, онда сызықтық тәуелділігі жоқ жазықтықта a, bвекторлары базис болады дейміз.
теңдігі орындалса, онда сызықтық тәуелділігі жоқ жазықтықта a, bвекторлары базис болады дейміз.
Кез келген коллинеар емес a, bвекторларыберілген жазықтықта базис болады. Мұның осылай болу себебі, алдыңғы кеңістіктегі базис сияқты көрсетіледі. Сөйтіп, a, b, cкеңістіктегі еркінше алынған базис, яғни кез келген компланар емес үш векторлар болады, ал a, b –жазықтықтағы кез келген коллинеар емес екі вектор, яғни бұл – жазықтықтағы базис болатын векторлар.
Енді аффиндік координаталар туралы ұғым берейік.
3-анықтама. Кеңістіктегі аффиндік координаталар a, b, cбазисінің және координаталардың бас нүктесінің (0) берілуімен анықталады. Кез келген М нүктесінің координаталары деп a, b, cбазисіне қарағандағы 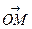 векторының координаталарын айтамыз. Әрбір
векторының координаталарын айтамыз. Әрбір 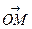 немесе Rвекторыa, b, cбазисіне жіктелетін болғандықтан, кеңістіктегі М нүктесіне үш аффиндік координаталар (x, y, z) сәйкес болу керек, яғни мына теңдік орындалады:
немесе Rвекторыa, b, cбазисіне жіктелетін болғандықтан, кеңістіктегі М нүктесіне үш аффиндік координаталар (x, y, z) сәйкес болу керек, яғни мына теңдік орындалады:
ax+by+cz-R=0.
Тік бұрышты координаталар аффиндік координаталардың дербес жағдайы болады. Тік бұрышты координаталарда базистік векторлар былайша белгіленеді: і, j, k.Бұларөз ара ортогонал және олардың модульдары бірге тең, яғни бұлар – орттар, бірлік векторлар. Осы жағдайда х, у, z үш саны тік бұрышты координаталар деп аталады және мына теңдік орындалады:
xі +yj +zk - R= 0
Егер М нүктесі кеңістіктегі кез келген нүкте болса, онда 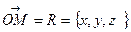 .
.
Дата добавления: 2015-08-20; просмотров: 3125;
